Artigo escrito por Danielly Santos
O que é Inferência Bayesiana?
A inferência estatística é utilizada para tirar conclusões sobre informações não observadas (parâmetros e previsões) a partir dos dados (amostra). Quando uma pesquisa eleitoral indica a intenção de voto por candidato, trata-se de uma inferência realizada a partir de uma amostra que visa representar a intenção de voto de todos os eleitores.
Pode-se dividir a estatística inferêncial em dois ramos: clássica (ou frequentista) e bayesiana. Na inferência clássica, todas as conclusões são feitas a partir dos dados coletados. Por outro lado, a inferência bayesiana acresenta informações conhecidas pelo pesquisador, assim, as informações subjetivas adicionadas podem incorporar conhecimento à inferência.
Por exemplo, na pesquisa eleitoral você sabe que nenhum candidato pode ter 100% dos votos. Então, usando inferência bayesiana, você pode incorporar essa informação ao modelo. No caso da inferência clássica, devemos assumir que tudo o que precisamos para realizar a inferência está disponível na amostra e, portanto, não incorporamos esse tipo de informação.
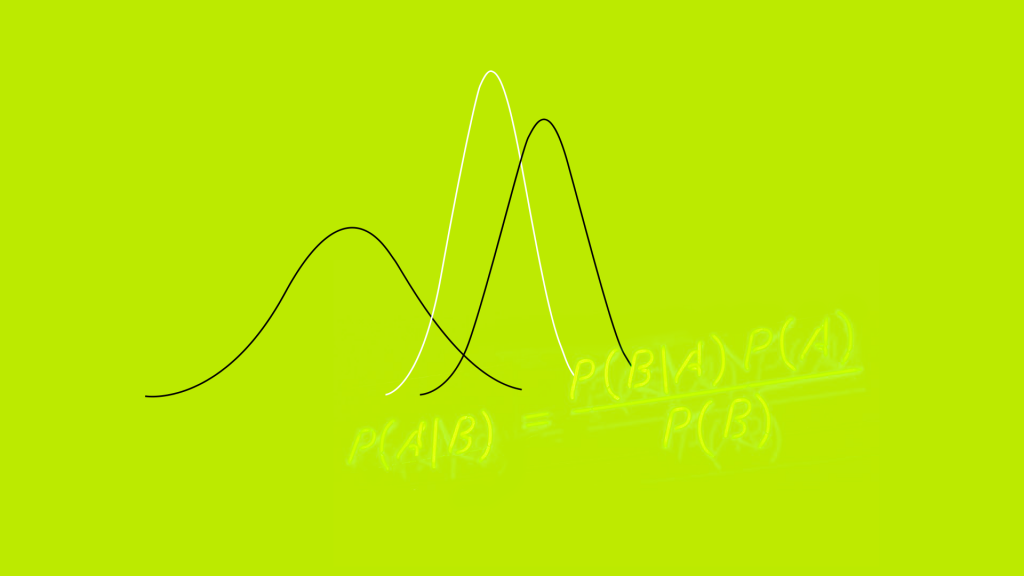
A inferência Bayesiana surgiu a partir do Teorema de Bayes. O Teorema de Bayes demostra como informações não contidas na amostra (chamada de informação a priori) podem ser incorporadas ao modelo.
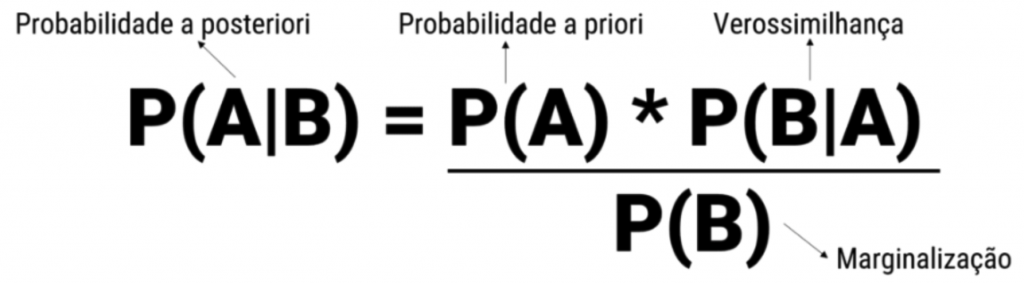
A partir do Teorema de Bayes pode-se calcular a probabilidade a posteriori de A ocorrer sabendo que B já aconteceu. A probabilidade a priori de A incorpora todo o conhecimento acumulado de estudos e eventos anteriores, enquanto a verossimilhança é uma função dos dados coletados (amostra).
Etapas da Inferência Bayesiana
1. Especificar um modelo probabilístico: Distribuição conjunta de todas as quantidades observadas e não observadas.
2. Obter a distribuição a posteriori: Distribuição das quantidades não observadas dado as quantidades observadas.
3. Verificar a adequação do modelo ajustado.
Discussão
A principal controvérsia em torno da inferência bayesiana está relacionada com como o conhecimento a priori pode enviesar as análises. Imagine que você adimita que nenhum candidato pode ter 70% dos votos, mas alguém alcança essa quantidade. Isso pode enviesar as estimativas da inferência.
Portanto, as informações devem ser incorporadas de forma criteriosa para que a inferência Bayesiana seja bem feita. Uma alternativa é utilizar distribuições a priori não informativas, como a distribuição a priori de Jeffreys que permite agregar a matriz de informação de Fisher.
Segundo o estatístico George Box: “Todos os modelos estão errados, mas alguns são úteis.”
Referências
