Artigo escrito por Bruno Miguel Albuquerque
Árvores Binárias de Busca (BST, do inglês Binary Search Tree) são estruturas de dados em forma de árvore, composta por nós interligados. Cada nó pode ter no máximo dois filhos, geralmente denominados “esquerdo” e “direito”. Cada nó da árvore contém um valor ou informação associada, e os nós filhos são organizados de acordo com uma relação de ordem.
As Árvores Binárias são estruturas eficientes para busca, inserção e remoção de elementos, permitindo a recuperação rápida dos dados armazenados.

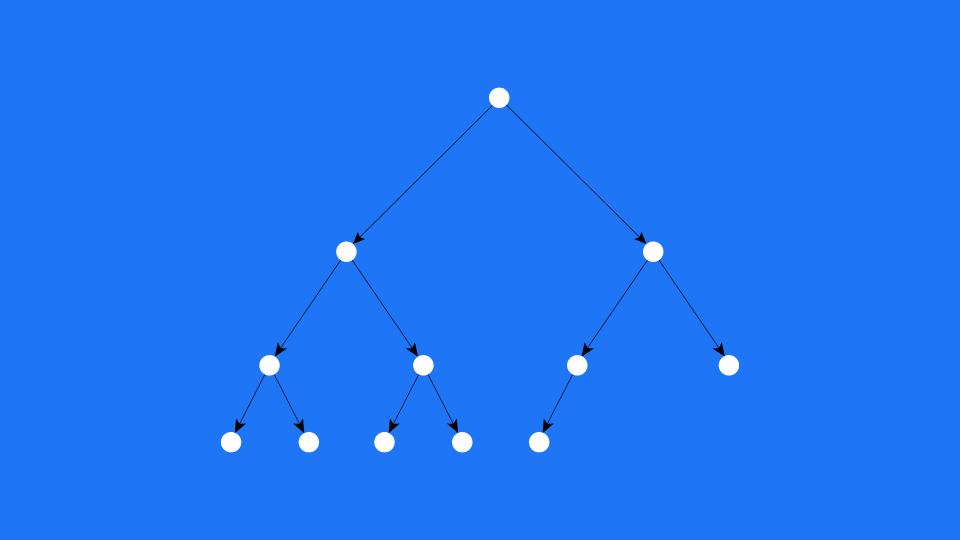
Por exemplo, nesta árvore, observamos que os elementos estão dispostos em ordem alfabética. Uma característica visível nas árvores binárias é que a letra “A”, primeiro termo da ordem alfabética, está no nó mais à esquerda, enquanto a letra “L”, o maior termo em ordem alfabética dentre os que estão representados na árvore, está no nó mais à direita.
Importância para a Ciência de Dados
Eficiência na busca e inserção: a Árvore Binária de Busca permite buscar e inserir elementos de forma eficiente, com uma complexidade O(log n). Isso é especialmente útil ao lidar com grandes volumes de dados, pois uma busca rápida é essencial em muitos algoritmos de Ciência de Dados.
Ordenação de dados: essa estrutura mantém os elementos ordenados de acordo com uma chave, o que é muito útil em cenários onde os dados precisam estar ordenados, como em séries temporais.
Aplicação em algoritmos de Aprendizado de Máquina: as árvores são fundamentais em muitos algoritmos de Aprendizado de Máquina, como árvores de decisão e florestas aleatórias.
Neste artigo, vamos explicar como construir uma Árvore de Busca Binária Balanceada (AVL tree) em Python.
Primeiros passos
Criar classe para representar o nó

Primeiramente, você deve criar uma classe para criar o nó, pois cada termo na árvore binária é representado por um nó, o qual se liga com seu termo a esquerda e com seu termo a direita, caso haja.
Função de inserir nó

Primeiramente, criamos a classe para representar a árvore de busca binária e depois criamos a função de adição de um nó a ela. Observe que essa função também confere o balanceamento da árvore a cada adição de termo.
Função de remover nó
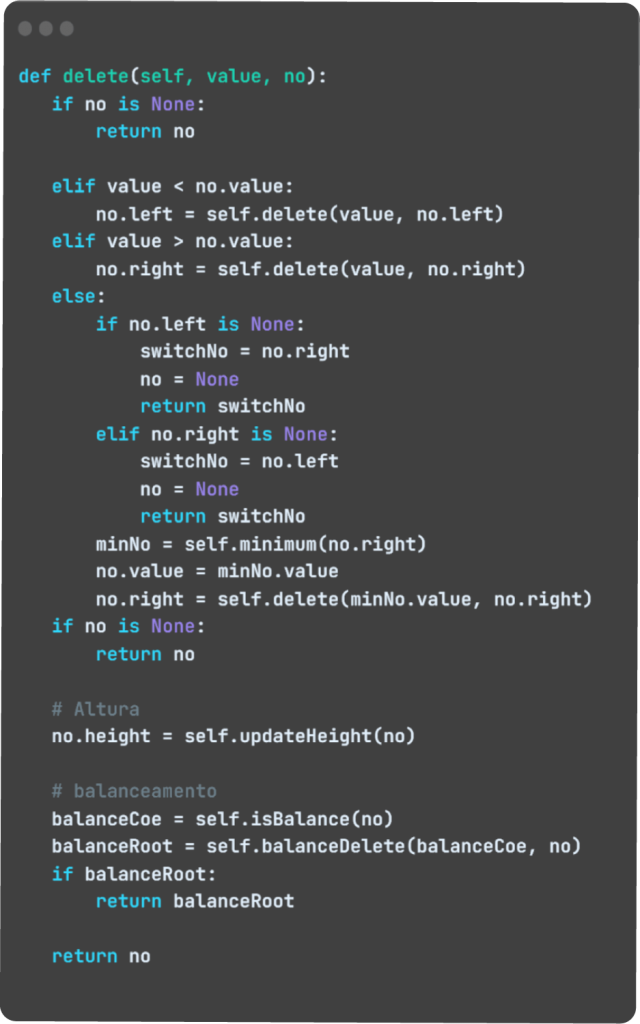
Primeiramente, criamos a função de remoção de nó na classe BST. Observe que essa função também confere o balanceamento da árvore a cada remoção, assim como a função de inserir.
Função de busca
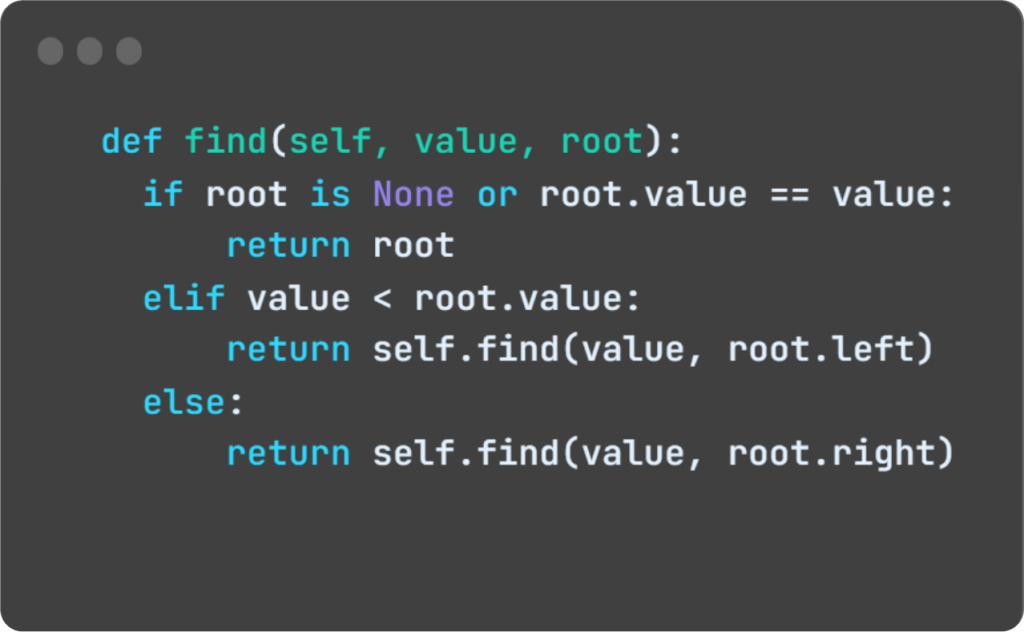
A função de busca recebe como parâmetro um valor e retorna o nó, ao qual esse valor pertence.
Funções de máximo e mínimo
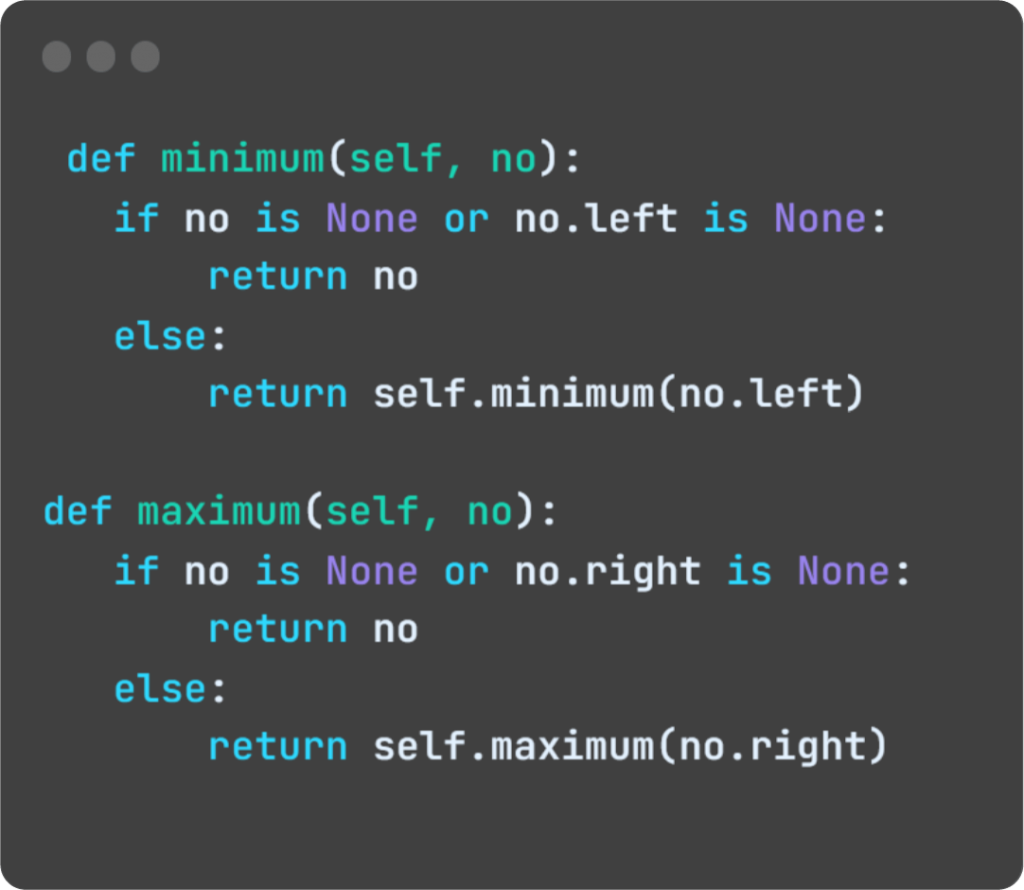
Essas funções retornam o nó de menor valor (localizado mais à esquerda) e o de maior valor (localizado mais à direita) da árvore.
Funções relacionadas à altura

A primeira retorna o valor da altura e a segunda atualiza o valor de altura de um nó.
Funções de rotação
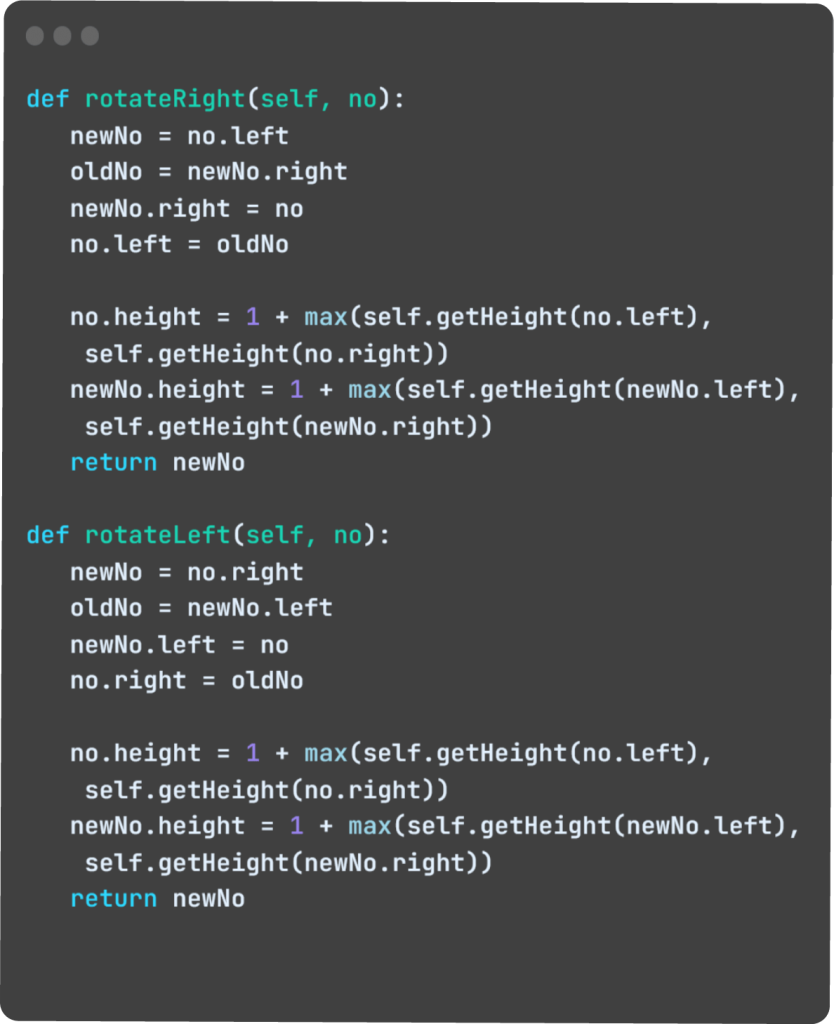
Tais funções são fundamentais para garantir que a árvore fique balanceada.
Funções relacionadas ao balanceamento
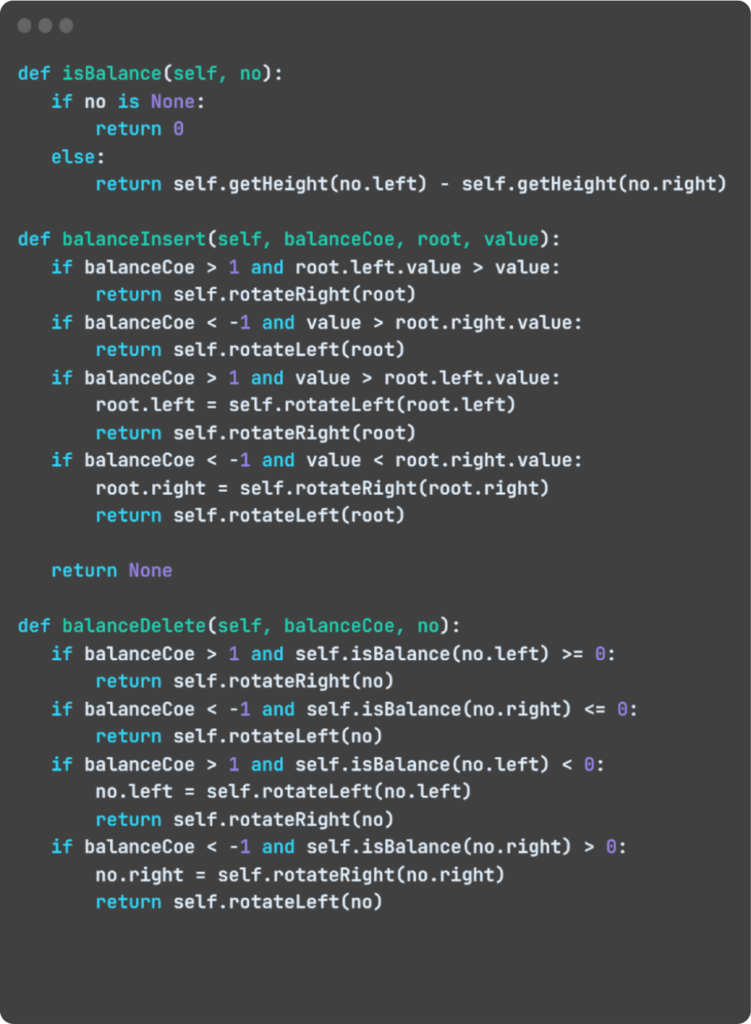
Essas funções conferem se a árvore está balanceada nas funções de inserir e deletar, e, caso não estejam, é realizada uma rotação na árvore.
Conclusão
Em resumo, uma árvore binária de busca desempenha um papel importante na ciência de dados, fornecendo uma estrutura eficiente para busca, inserção, ordenação e operações baseadas em intervalo. Sua organização em forma de árvore e a relação de ordem entre os nós garantem um acesso rápido aos dados armazenados, sendo amplamente utilizada em diversas aplicações, como bancos de dados, algoritmos de busca e classificação, entre outros.
Referências
CORMEN, T. H. et.al. Algoritmos: teoria e prática, 3 edição. Ed. Campus, 2002. (CLRS)