Artigo escrito por Arthur Gontijo
O Paradoxo de Simpson é um fenômeno estatístico que revela como uma análise de dados simples pode enganar. Quando olhamos apenas para dados agregados, muitas vezes ignoramos fatores ocultos que influenciam os resultados, distorcendo completamente o que percebemos como tendências. Por isso, quem busca interpretar os dados de forma precisa deve compreender esse paradoxo.
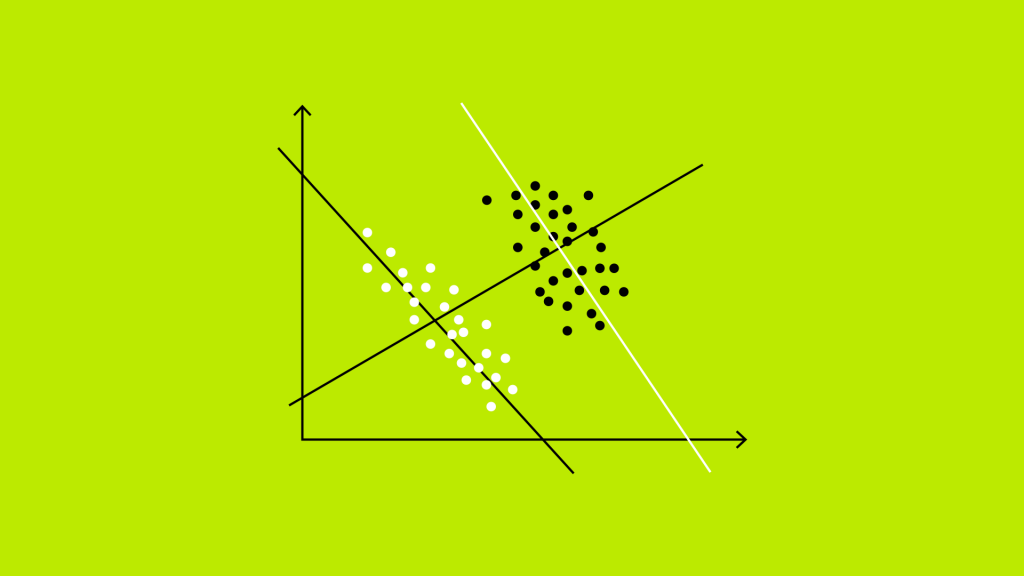
Ao trabalharmos com dados, é de extrema importância evitar conclusões precipitadas, pois fatores não evidentes podem enganar nossas interpretações. Uma das armadilhas mais notórias é o Paradoxo de Simpson. Esse fenômeno ocorre quando uma tendência clara em subgrupos é invertida ou desaparece ao analisarmos os dados de forma agregada. Em outras palavras, a correlação ou associação observada entre as variáveis nos diz algo quando agregamos os dados, e nos diz o completo oposto quando os subdividimos, criando assim o paradoxo.
Isso se deve à influência de uma “variável de confusão” — um fator ignorado inicialmente, mas que afeta tanto as variáveis independentes quanto dependentes. Dessa forma, identificar essa variável é crucial para para determinarmos com qual lado paradoxo iremos ficar, e assim, descobrirmos a verdadeira associação entre as variáveis.
Um Exemplo Prático do Paradoxo de Simpson
Agora, vamos ver um exemplo prático: imagine que você deseja estudar o impacto da preparação para uma prova de estatística no desempenho dos alunos. Para isso, você seleciona aleatoriamente estudantes de uma universidade e aplica essa prova. Os alunos são informados sobre o conteúdo e incentivados a estudar, registrando o número de horas dedicadas ao estudo até a data do teste. Após aplicar a prova, você observa algo intrigante: os alunos que estudaram menos obtiveram as melhores notas.
Surpreso, você calcula a correlação entre as horas de estudo e as notas e obtém um valor fortemente negativo (-0,7915). Para investigar, você decide segmentar os dados por curso. Analisando cada curso individualmente, você percebe que, na verdade, quanto mais horas os alunos passaram estudando, melhores foram suas notas. Ou seja, ao segmentar os dados por curso, a relação entre as variáveis ‘nota na prova’ e ‘horas de estudo’ se inverte, indicando a presença do Paradoxo de Simpson.
Neste caso, a variável de confusão é a familiaridade dos alunos com o tema da prova. Alunos do curso de estatística e de cursos relacionados, por já terem mais contato com o conteúdo, estudam menos e, ainda assim, obtêm notas altas, pois estão mais confiantes. Em contraste, alunos de outros cursos, menos familiares com o conteúdo, precisam estudar mais para obter um desempenho similar.
A Conclusão e o Impacto da Análise Segmentada
Assim, a verdadeira conclusão é que, dentro de cada curso, existe uma relação positiva entre horas de estudo e nota: quem estuda mais tende a ter notas melhores. No entanto, na análise agregada, ou seja, de todos os cursos juntos sem segmentação, o efeito da familiaridade com o conteúdo cria uma correlação negativa ilusória. Essa distorção causada pelo Paradoxo de Simpson demonstra a importância de segmentar e analisar os dados com cautela, evitando conclusões superficiais.
A Importância da Análise Cuidadosa e das Variáveis de Confusão
O Paradoxo de Simpson reforça que dados isolados não são suficientes para responder a uma pergunta de pesquisa. É fundamental conhecer o contexto e considerar possíveis variáveis de confusão antes de tirar conclusões equivocadas ou até mesmo deliberadamente maliciosas. Imagine se o estudo hipotético fosse divulgado com a afirmação: “Mais horas de estudo afetam negativamente a performance acadêmica”. Seria uma conclusão errônea, ignorando o efeito do conhecimento prévio sobre o tema.
O paradoxo nos ensina que dados exigem uma interpretação cuidadosa, unindo análise técnica e compreensão do contexto. Combinar dados com hipóteses sobre causalidade é essencial para alcançar respostas precisas e evitar conclusões enganosas.
Referências
minutephysics. “Simpson’s Paradox.” YouTube, 24 out. 2017, Disponível em: www.youtube.com/watch?v=ebEkn-BiW5k. Acessado em: 25/10/2024
DUMARAIS, Maxime. Simpson’s paradox: how to prove two opposite arguments using one dataset. Towards Data Science, 2020. Disponível em: https://towardsdatascience.com/simpsons-paradox-how-to-prove-two-opposite-arguments-using-one-dataset-1c9c917f5ff9. Acesso em: 25 out. 2024.