Artigo escrito por Paula Gouveia
No primeiro artigo sobre regressão logística simples, apresentamos o Caso 1, no qual exploramos a construção de um modelo para prever a ocorrência de doenças coronárias (CHD) com base na idade dos pacientes. Analisamos como preparar os dados, ajustar o modelo e interpretar os coeficientes estimados. Agora, daremos continuidade à nossa abordagem de regressão logística, aplicando-a a um novo contexto: a previsão da presença de um sintoma cognitivo em idosos com base no escore obtido em um exame psicológico.
Neste estudo, ajustaremos um modelo para compreender a relação entre o escore do exame e a probabilidade de ocorrência do sintoma de caduquice. Além disso, exploraremos a interpretação dos coeficientes, calcularemos a razão de chances e avaliaremos a precisão das estimativas por meio do intervalo de confiança. Essa análise nos ajudará a entender melhor como variáveis explicativas podem influenciar resultados binários e como a regressão logística pode ser aplicada a diferentes cenários.
O objetivo deste estudo é ajustar um modelo de regressão logística simples para prever a ocorrência do sintoma com base no escore do exame. Vamos realizar a análise dos dados, interpretar os resultados do modelo e tirar algumas conclusões relevantes.
1. Instalação e Importação das Bibliotecas
Para realizar essa análise, utilizamos as bibliotecas pandas, numpy, matplotlib, seaborn para visualizações de dados e manipulação e statsmodels para regressão. Caso alguma dessas não esteja instalada, utilize o seguinte comando para instalar o statsmodels:
pip install statsmodelsAgora, vamos importar as bibliotecas necessárias:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf2. Conjunto de Dados
Para cada indivíduo, temos um escore de um exame psicológico, que será nossa variável explicativa/independente, denominada escore, representando o resultado do exame. Além disso, temos a variável resposta/dependente, denominada resp_sintoma, que indica a presença ou ausência do sintoma de caduquice.
escore: escore obtido no exame psicológico;resp_sintoma: variável binária indicando presença (1) ou ausência (0) do sintoma.
Utilizamos o Python para estruturar nossos dados, criando um DataFrame que captura essas informações:
# Dados
# Variável explicativa/independente
escore = [9, 13, 6, 8, 10, 4, 14,
8, 11, 7, 9, 7, 5, 14,
13, 16, 10, 12, 11, 14, 15,
18, 7, 16, 9, 9, 11, 13,
15, 13, 10, 11, 6, 17, 14,
19, 9, 11, 14, 10, 16, 10,
16, 14, 13, 13, 9, 15, 10,
11, 12, 4, 14, 20]# Variável resposta/dependente
# 1 = presença de sintoma & 0 = ausência de sintoma
resp_sintoma = [1] * 14 + [0] * 40Criaremos um DataFrame com essas duas variáveis, que iremos atribuir o nome de caduquice. Esse DataFrame, então, será composto pela variável escore e pela variável resp_sintoma:
# Criar o DataFrame
caduquice = pd.DataFrame({'escore': escore, 'resp_sintoma': resp_sintoma})Assim, temos um conjunto de dados composto por 54 indivíduos idosos e duas variáveis de interesse: o escore e a variável binária resp_sintoma.
3. Análise Exploratória
Antes de ajustar o modelo, é fundamental analisarmos o comportamento geral dos dados. Para isso, primeiramente, calculamos algumas medidas de resumo:
# Medidas resumo
print("Resumo do DataFrame:")
print(caduquice.describe())
print("\nFrequência da variável resposta:")
print(caduquice['resp_sintoma'].value_counts())A função describe fornece um resumo estatístico das variáveis, exibindo informações essenciais, como média, desvio padrão, valores mínimos e máximos. Além disso, a função value_counts nos permite visualizar a distribuição dos valores da variável resp_sintoma, que representa a presença ou ausência do sintoma.
Resumo do DataFrame:
escore resp_sintoma
count 54.000000 54.000000
mean 11.574074 0.259259
std 3.709253 0.442343
min 4.000000 0.000000
25% 9.000000 0.000000
50% 9.000000 0.000000
75% 14.000000 0.750000
max 20.000000 1.000000
Frequência da variável resposta:
resp_sintoma
0 40
1 14
Name: count, dtype: int64Com base nesses resultados, podemos tirar algumas conclusões importantes.
Em primeiro lugar, observamos que o escore varia entre 4 (mínimo) e 20 (máximo), com uma média de 11,57. Além disso, ao analisarmos os quartis, percebemos que 50% das observações apresentam um escore igual ou menor que 11, enquanto 75% das observações têm um escore igual ou menor que 14.
Outro ponto relevante é a distribuição da variável resposta. Notamos que 40 idosos não apresentaram sintoma (0), enquanto 14 apresentaram (1). Isso indica que a presença do sintoma ocorre em cerca de 26% da amostra, o que pode ser um fator importante para a análise futura.
3.1 Visualização da Relação entre Escore e Sintoma
Para compreender melhor essa relação, utilizamos um gráfico de dispersão. Dessa forma, podemos visualizar como os valores do escore estão distribuídos entre aqueles que apresentaram (1) e não apresentaram (0) sintomas.
# Gráfico
plt.scatter(caduquice['escore'], caduquice['resp_sintoma'], alpha=0.7)
plt.xlabel('Escore')
plt.ylabel('Resp Sintoma')
plt.title('Relação entre escore e sintoma')
plt.show()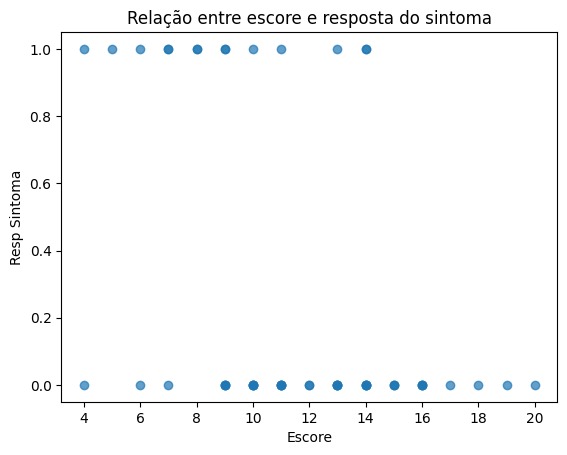
Esse gráfico nos permite identificar possíveis padrões entre o escore e a presença do sintoma. Se houver uma tendência clara, isso pode indicar uma possível relação entre essas variáveis, o que pode ser explorado em análises mais aprofundadas.
Dessa forma, com essa análise inicial, conseguimos obter uma visão geral dos dados, facilitando os próximos passos no processo de modelagem.
4. Ajuste do Modelo de Regressão Logística
Para explicar a ocorrência do sintoma em função do escore, utilizamos a regressão logística por meio da biblioteca statsmodels. Essa abordagem é ideal para lidar com variáveis binárias, como é o caso da variável que representa a presença ou ausência do sintoma. Além disso, a função summary() nos permite visualizar os resultados detalhados do modelo, incluindo coeficientes, erros padrões, valores p e outras estatísticas relevantes.
Dessa forma, ajustamos o modelo conforme o código abaixo:
# Ajuste do modelo logístico
modelo = smf.logit("resp_sintoma ~ escore", data=caduquice).fit()
print("\nResumo do modelo:")
print(modelo.summary())O processo de otimização foi bem-sucedido após seis iterações, e os principais resultados do modelo são apresentados a seguir:
Optimization terminated successfully.
Current function value: 0.472383
Iterations 6
Resumo do modelo:
---------------------------------------------------------------------------------
Logit Regression Results
---------------------------------------------------------------------------------
Dep. Variable: resp_sintoma No. Observations: 54
Model: Logit Df Residuals: 52
Method: MLE Df Model: 1
Date: Fri, 07 Feb 2025 Pseudo R-squ.: 0.1746
Time: 14:25:26 Log-Likelihood: -25.509
converged: True LL-Null: -30.903
Covariance Type: nonrobust LLR p-value: 0.00121
---------------------------------------------------------------------------------
coef std err z P>|z| [0.025 0.975]
_________________________________________________________________________________
Intercept 2.4040 1.192 2.017 0.044 0.068 4.740
escore -0.3235 0.114 -2.838 0.005 -0.547 -0.100
---------------------------------------------------------------------------------Ao analisar o resumo do modelo, podemos destacar alguns pontos importantes:
- Intercepto: O coeficiente do intercepto é 2,40. Embora esse valor seja reportado, ele não tem um significado prático para este resultado.
- Coeficiente do escore: O coeficiente associado à variável
escoreé -0,32, o que significa que há uma relação inversa entre o escore e a ocorrência do sintoma. Além disso, o valor p associado a esse coeficiente é 0,005, o que indica que ele é estatisticamente significante dentro do modelo proposto.
Nesse sentido, para verificar a significância da variável, utilizamos o valor p. Como ele é menor que 0,05, podemos concluir que o escore tem um impacto relevante na explicação da ocorrência do sintoma.
Outro ponto essencial é que os coeficientes da regressão logística são apresentados na forma logarítmica. Assim, o coeficiente de -0,32 indica que o logaritmo da razão de chances diminui com o aumento do escore. No entanto, essa interpretação pode ser pouco intuitiva. Por isso, é mais interessante calcular o odds ratio (razão de chances), que facilita a compreensão do impacto do escore na probabilidade de ocorrência do sintoma.
5. Cálculo da Razão de Chances (Odds Ratio)
Para transformar os coeficientes em razões de chance, utilizamos a função np.exp(), conforme demonstrado abaixo:
# Odds Ratio (Razão de Chances)
odds_ratio = np.exp(modelo.params)
print("\nOdds Ratios:")
print(odds_ratio)Os resultados obtidos são os seguintes:
Odds Ratios:
Intercept 11.067837
escore: 0.723590
dtype: float64Isso significa que, para cada unidade adicional no escore, a chance de apresentar o sintoma diminui em uma proporção correspondente a um odds ratio de 0,72. Ou seja, à medida que o escore aumenta, a probabilidade de ocorrência do sintoma reduz.
Além disso, podemos calcular a variação percentual dessa redução, o que torna a interpretação ainda mais clara:
# Cálculo da variação percentual
variacao_percentual = (1 - odds_ratio['escore']) * 100
print(f"Variação percentual: {variacao_percentual:.2f}%")Com isso, encontramos que a cada aumento unitário no escore, a chance de apresentar o sintoma diminui em aproximadamente 27,64%.
6. Intervalo de Confiança
Por fim, para avaliar a precisão das estimativas, calculamos o intervalo de confiança de 95% para os coeficientes:
# Intervalo de Confiança (95%)
conf = modelo.conf_int()
conf['OR'] = odds_ratio
conf.columns = ['2.5%', '97.5%', 'OR']
conf[['OR', '2.5%', '97.5%']] = np.exp(conf[['OR', '2.5%', '97.5%']])
print("\nIntervalo de Confiança (95%):")
print(conf)Os resultados obtidos são os seguintes:
Intervalo de Confiança (95%):
2.5% 97.5% OR
Intercept 1.070461 114.433901 64076.751025
escore 0.578726 0.904716 2.061822Isso significa que, com 95% de confiança, a verdadeira razão de chances do escore está entre 0,56 e 0,88. Esse intervalo reforça a ideia de que o escore reduz significativamente a chance de ocorrência do sintoma, pois os limites do intervalo estão abaixo de 1.
Conclusão
Neste estudo, ajustamos um modelo de regressão logística simples para prever a ocorrência de caduquice em idosos com base no escore obtido em um exame psicológico. Ao analisar o coeficiente do escore, observamos que ele tem uma relação inversa com a probabilidade de ocorrência do sintoma. O cálculo da razão de chances revelou que, a cada aumento unitário no escore, a probabilidade de apresentação do sintoma diminui em aproximadamente 27,64%. Esse achado sugere que escores mais altos no exame psicológico estão associados a uma menor probabilidade de o indivíduo apresentar sinais de caduquice.
Além disso, a utilização do intervalo de confiança nos permitiu avaliar a precisão das estimativas, fornecendo uma visão mais robusta sobre os efeitos da variável explicativa.
A partir deste modelo, podemos fazer previsões mais informadas sobre a probabilidade de um idoso apresentar o sintoma, com base em seu escore no exame. Como próxima etapa, seria interessante explorar outras variáveis explicativas que possam aprimorar ainda mais a acurácia do modelo.
Você também pode aprender mais sobre esse tema pelo nosso canal no YouTube! Assista ao vídeo sobre Regressão Logística Simples em Python (Caso 2) no canal da Statplace.
Referências Bibliográficas
AGRESTI, A. An introduction to categorical data analysis. 2. ed. New York: J. Wiley & Sons, 2007. 394 p.
AGRESTI, A. Categorical data analysis. 3. ed. New York: J. Wiley & Sons, 2013. 714 p.
GIOLO, S. R. Introdução à análise de dados categóricos com aplicações. São Paulo: Blucher, 2017. 256 p.
HOSMER, D.; LEMESHOW, S.; STURDIVANT, R. Applied Logistic Regression. 3. ed. New York: J. Wiley & Sons, 2013. 528 p.