Testes para comparação de proporções

Artigo escrito com a colaboração de Lara Reis

Os testes de hipótese fazem parte da estatística inferencial que é usada para formular conclusões e fazer inferências sobre as populações baseados em dados de amostras coletados em pesquisas. Os testes para proporções são utilizados quando temos duas variáveis em escala nominal ou ordinal. Eles visam responder as seguintes perguntas:

1. A amostra é semelhante a população que a originou? A frequência observada de um evento em uma amostra é igual a frequência com que ele é esperado?
2. As variáveis comparadas são independentes? Há associação entre as variáveis? Será que uma característica está associada com a ocorrência de certo evento?
3. Será que diferentes amostras têm a mesma proporção de indivíduos com alguma característica?
4. Após a aplicação de um tratamento, houve mudanças significativas de uma categoria para outra? Houve mudanças de uma característica ao longo do tempo.

Para cada pergunta a um teste específico:

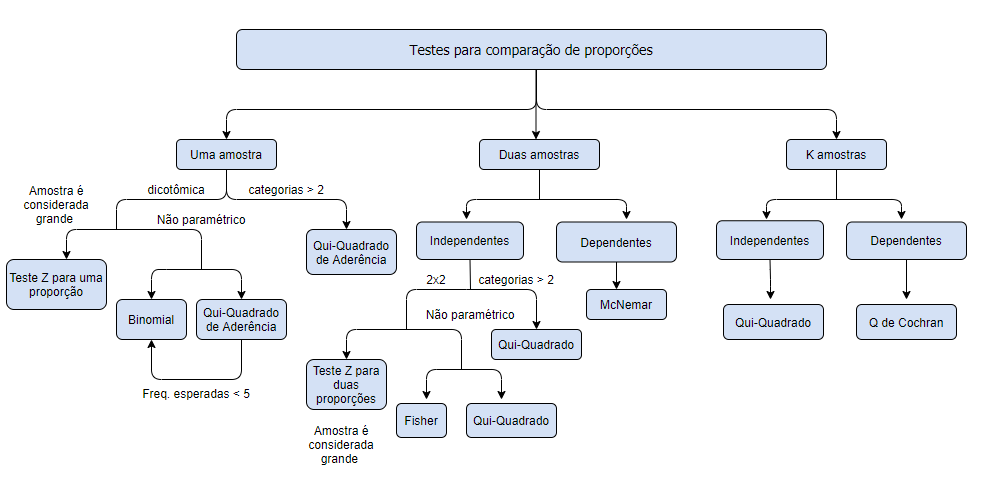
Testes para uma amostra

Os testes para comparação de uma amostra é utilizado para verificar se uma determinada amostra vem de uma população especificada. Podem ser chamados de testes de aderência ou bondade do ajuste, uma vez que compara-se a distribuição amostral com a distribuição de interesse.

É importante para uma análise, uma vez que a semelhança da amostra com a população que a originou possibilita que os resultados da análise sejam mais fidedignos.

Há três testes para comparar proporção em uma amostra:

Teste Binomial

Para a realização do teste binomial é necessário que a variável seja dicotômica, ou seja, assuma apenas dois valores (categorias). Seu intuito é verificar se a proporção de sucessos (presença de uma característica) observada na amostra (pˆ) pode pertencer a uma população com uma determinada proporção.

Requisitos:

• Cada observação é classificada como sucesso (X = 1) ou fracasso (X = 0).
• As n tentativas são independentes.
• Cada tentativa tem probabilidade p de sucesso.

Estatítica de teste:

Y = número de sucessos.

Hipóteses:

H₀ : p = p₀
H₁ : p ≠ p₀

H₀ : p = p₀
H₁ : p < p₀

H₀ : p = p₀
H₁ : p > p₀

Exemplos :

• Um industria textil afirma que seu processo de fabricação produz 95% de produtos dentro das especificações. Deseja-se averiguar se este processo ainda está sob controle. Uma amostra de 20 produtos foi analisada e foram constatadas 14 produtos dentro das especificações. Ao nível de 5% de significância, podemos afirmar que realmente o processo produz 95% de produtos dentro das especificações?

H₀ : p = 0,95
H₁ : p ≠ 0,95

• Estima-se que cerca de 40% das mulheres que são submetidas à cirurgia do câncer de mama têm algum tipo de efeito após a cirúgia. Um novo método de cirurgia foi realizado em 18 pacientes e 4 tiveram algum efeito. Ao nível de 5% de significância, podemos afirmar que o novo método é eficiente na redução dos efeitos?

H₀ : p = 0,40
H₁ : p < 0,40

Aplicação no R:

binom.test (Y, n, p0, alternarive= c(“greater”, “less”, “two-sided”), conf.level)

binom.test(14, 20, p = 0.95, alternative = c( "two.sided"),conf.level = 0.95)

## 
##  Exact binomial test
## 
## data:  14 and 20
## number of successes = 14, number of trials = 20, p-value = 0.0003293
## alternative hypothesis: true probability of success is not equal to 0.95
## 95 percent confidence interval:
##  0.4572108 0.8810684
## sample estimates:
## probability of success 
##                    0.7

binom.test(4, 18, p = 0.40, alternative = c( "less"),conf.level = 0.95)

## 
##  Exact binomial test
## 
## data:  4 and 18
## number of successes = 4, number of trials = 18, p-value = 0.09417
## alternative hypothesis: true probability of success is less than 0.4
## 95 percent confidence interval:
##  0.0000000 0.4388828
## sample estimates:
## probability of success 
##              0.2222222

Teste Z para proporção

Quando a amostra é considerada grande pode-se utilizar a aproximação da Binomial pela distribuição Normal através do Teorema Central do Limite, logo o número de sucessos:

Y ∼ Normal (np, np(1−p))

O ideal é que seja feita uma correção de continuidade em razão de se aproximar a distribuição Binomial, que é discreta, por uma distribuição Normal, que é contínua.

Estatística de teste:

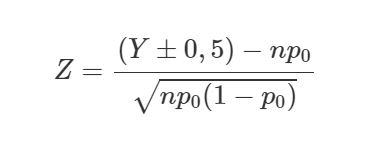
Quando Y ≤ np utiliza-se Y + 0,5.

Quando Y ≥ np utiliza-se Y − 0,5.

Hipóteses:

H₀ : p = p₀
H₁ : p ≠ p₀

H₀ : p = p₀
H₁ : p < p₀

H₀ : p = p₀
H₁ : p > p₀

Exemplos:

• Um industria textil afirma que seu processo de fabricação produz 95% de produtos dentro das especificações. Deseja-se averiguar se este processo ainda está sob controle. Uma amostra de 150 produtos foi analisada e foram constatadas 130 produtos dentro das especificações. Ao nível de 5% de significância, podemos afirmar que realmente o processo produz 95% de produtos dentro das especificações?

H₀ : p = 0,95
H₁ : p ≠ 0,95

• Estima-se que cerca de 40% das mulheres que são submetidas à cirurgia do câncer de mama têm algum tipo de efeito após a cirúgia. Um novo método de cirurgia foi realizado em 60 pacientes e 15 tiveram algum efeito. Ao nível de 5% de significância, podemos afirmar que o novo método é eficiente na redução dos efeitos?

H₀ : p = 0,40
H₁ : p < 0,40

Aplicação do R:

#prop.test(y,n,p,coef.level, alt=)

prop.test(130,150,0.95, conf.level = 0.95, correct = TRUE, alt="two.sided")

## 
##  1-sample proportions test with continuity correction
## 
## data:  130 out of 150, null probability 0.95
## X-squared = 20.211, df = 1, p-value = 6.937e-06
## alternative hypothesis: true p is not equal to 0.95
## 95 percent confidence interval:
##  0.7992288 0.9147007
## sample estimates:
##         p 
## 0.8666667

prop.test(15,60,0.40,conf.level = 0.95,  correct = TRUE, alt="less")

## 
##  1-sample proportions test with continuity correction
## 
## data:  15 out of 60, null probability 0.4
## X-squared = 5.0174, df = 1, p-value = 0.01255
## alternative hypothesis: true p is less than 0.4
## 95 percent confidence interval:
##  0.0000000 0.3602784
## sample estimates:
##    p 
## 0.25

Teste Qui-Quadrado de Aderência

É usado para comparar dados amostrais com dados de populações conhecidas. Consiste em verificar se a frequência observada difere significativamente da frequência esperada (geralmente especificada por uma distribuição de probabilidade).

Requisitos:

• As observações devem ser independentes;
• Se o número de categorias é igual a 2 as frequências esperadas devem ser superiores a 5;
• Se o número de categorias for maior que 2, não devem ter mais de 20% das frequências esperadas inferior a 5 e nenhuma frequência esperada igual a zero;
• Para evitar frequências esperadas pequenas deve-se combinar as categorias até que as exigências sejam atendidas. Caso as categorias sejam combinadas em apenas duas e mesmo assim as exigências não sejam atendidas, deve-se utilizar o Teste Binomial.

OBS: O pressuposto para valores esperados deve-se ao fato de que a distribuição amostral é assintoticamente Qui-quadrado, ou seja, ela tende a ter distribuição Qui-Quadrado quando as frequências são grandes (tendem ao infinito).

Hipóteses:

H₀: os dados têm distribuição especificada.
H₁: os dados não têm distribuição especificada.

Estatística de teste:

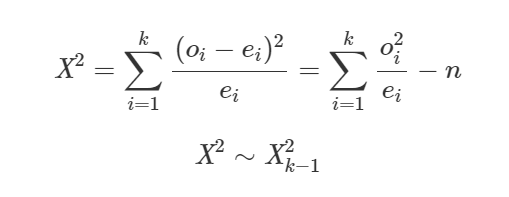
Onde:

• k é o número de categorias da variável
• o_i é a frequência observada na categoria i;
• e_i é a frequência esperada na categoria i;
• e_i = nP(X = x);

OBS: Quanto maior for a diferença entre as frequências observadas e as frequências esperadas, maior é o valor da estatística de teste, e portanto, mais favoravel é a rejeição da H₀.

Exemplo 1:

Um estudo sobre os acessos ao blog da Oper nos sete dias da semana revelou que em 210 acessos: segunda: 35, terça: 40, quarta: 20, quinta: 28 ,sexta: 33, sabado: 28 e domingo:26. O objetivo é testar a hipótese que os acessos ao blog ocorrem com igual frequência nos sete dias da semana ao nivel de 5% de significância.

H₀ : p₁ = p₂ = p₃ = p₄ = p₅ = p₆ = p₇ = 1/7
H₁ : p_j ≠ 1/7

n = 210
f_obs = c(35,40,20,28,33,28,26)
prob = rep(1/7,7)
chisq.test(f_obs,p = prob)

## 
##  Chi-squared test for given probabilities
## 
## data:  f_obs
## X-squared = 8.6, df = 6, p-value = 0.1974

Exemplo 2:

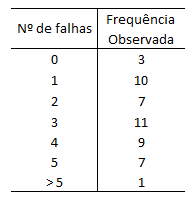
Através da realização de um experimento de 48 horas em um processo de produção, foi observado o número de falhas mecânicas por hora nos aparelhos, os valores estão abaixo. Um engenheiro afirma que o processo descrito, seguem uma distribuição de Poisson com média igual a 3. Testar com α=0.05.

H₀: as falhas mecânicas seguem uma distribuição Poisson (3).
H₁: as falhas mecânicas não seguem uma distribuição Poisson (3).

f_obs_falhas = c(3,10,7,11,9,7,1) 
n_falhas = c(0,1,2,3,4,5)
prob = dpois(n_falhas, 3) 
x = 1-sum(prob) 
prob2 = c(prob,x) 
f_esp = 48*prob2
f_esp

## [1]  2.389779  7.169338 10.754007 10.754007  8.065505  4.839303  4.028061

chisq.test(f_obs_falhas,p=prob2)

## Warning in chisq.test(f_obs_falhas, p = prob2): Chi-squared approximation may be
## incorrect

## 
##  Chi-squared test for given probabilities
## 
## data:  f_obs_falhas
## X-squared = 5.9388, df = 6, p-value = 0.4301

#como há 20% de celulas com frequências esperadas menores que 5, devemos agrupar

f_obs_falhas = c(3,10,7,11,17) 
n_falhas = c(0,1,2,3)
prob = dpois(n_falhas, 3) 
x=1-sum(prob) 
prob2=c(prob,x) 
chisq.test(f_obs_falhas,p=prob2)$expected

## Warning in chisq.test(f_obs_falhas, p = prob2): Chi-squared approximation may be
## incorrect

## [1]  2.389779  7.169338 10.754007 10.754007 16.932869

chisq.test(f_obs_falhas,p=prob2)

## Warning in chisq.test(f_obs_falhas, p = prob2): Chi-squared approximation may be
## incorrect

## 
##  Chi-squared test for given probabilities
## 
## data:  f_obs_falhas
## X-squared = 2.5898, df = 4, p-value = 0.6286

O chisq.test avisa quando há frequências esperadas pequenas, porém pode ser verificado que apenas uma frequência esperada foi menor que 5. De acordo com os pressupostos não devem ter mais de 20% das frequências esperadas inferior a 5, ou seja, não pode haver mais que 1 categoria com frequência esperada menor que 5.

Duas amostras

Amostras independentes

Teste Exato de Fisher (2×2)

O Teste Exato de Fisher é utilizado em tabelas de contingência para comparar dois tipo de classificações de duas amostras independentes. Ele fornece valor-p exato e não exige técnica de aproximação, além de ser preciso para todos os tamanhos amostrais. Ele é baseado na distribuição hipergeométrica e, portanto, o valor-p é condicional sobre os totais marginais da tabela.

Hipóteses:

H₀ : p₁ = p₂
H₁ : p₁ ≠ p₂

H₀ : p₁ = p₂
H₁ : p₁ < p₂

H₀ : p₁ = p₂
H₁ : p₁ > p₂

H₀: as variáveis são independentes
H₁: as variáveis não são independentes

Estatística de teste:

A probabilidade de interesse é:

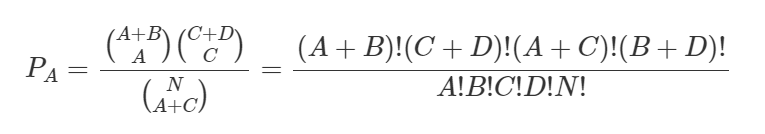
O teste Exato de Fisher calcula a probabilidade exata de ocorrência de uma frequência observada ou de valores mais extremos. Para isso, são feitas novos arranjos na qual a frequência da celula A vai diminuindo ou aumentando para que tenha mais discrepância em relação a hipotese nula. Assim para cada arranjo são calculadas PA (valor p) e depois são somadas.

Exemplo:

A obesidade tem sido apontada com um dos principais fatores de risco para a diabetes. Obteve-se então uma amostra de 23 pacientes. Ao nível de 5% de significância, há evidências de que obesidade e diabetes são associadas?

H₀: obesidade e diabetes são independentes.
H₁: obesidade e diabetes não são independentes (são associadas).

Aplicação no R

data_frame <- matrix(c(10,4, 2,7), nrow = 2,
                     dimnames = list("Obesidade" = c("Sim","Não"),
                                     "Diabetes" = c( "Sim","Não")))
data_frame

##          Diabetes
## Obesidade Sim Não
##       Sim  10   2
##       Não   4   7

prop.table(data_frame,2)

##          Diabetes
## Obesidade       Sim       Não
##       Sim 0.7142857 0.2222222
##       Não 0.2857143 0.7777778

fisher.test(data_frame, alternative = "two.sided", conf.level= 0.95)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  data_frame
## p-value = 0.03607
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##    0.9470815 110.2262775
## sample estimates:
## odds ratio 
##   7.827922

A função fisher.test fornece a razão de chance de um evento acontecer. Se estamos testando se as variáveis são independentes, estamos testando se a razão de chance é igual a 1, indicando que o evento é igualmente provável de acontecer em ambos os grupos.

Teste Z para duas proporções

Para amostras grandes pode-se usar o teste Z para duas proporções através da aproximação pela Normal de duas amostras com distribuição Bernoulli.

Hipóteses:

H₀ : p₁ − p₂ = 0
H₁ : p₁ − p₂ ≠ 0

H₀ : p₁ − p₂ = 0
H₁ : p₁ − p₂ < 0

H₀ : p₁ − p₂ = 0
H₁ : p₁ − p₂ > 0

Se não há associação entre as variáveis, esperamos que as proporções de sucesso sejam as mesmas nos dois grupos.

Através do Portal de Dados Abertos do Estado de Minas Gerais foi obtido dados referentes a casos confimados de COVID-19 entre março a julho de 2020. Deseja-se invertigar possíveis associações entre as caracteristicas e desfechos dos pacientes.

if(!require(tidyverse)){install.packages("tidyverse");require(tidyverse)}

#Banco de dados 
covid_MG <- read.csv('covid2.csv')
dim(covid_MG) 

## [1] 46446    19

covid_MG %>% head() %>% knitr::kable(caption = "A knitr kable.")

ï.._id	URS	MICRO	MACRO	ID	DATA_NOTIFICACAO	CLASSIFICACAO_CASO	SEXO	IDADE	FAIXA_ETARIA	MUNICIPIO_RESIDENCIA	CODIGO	COMORBIDADE	EVOLUCAO	INTERNACAO	UTI	RACA	DATA_ATUALIZACAO	ORIGEM_DA_INFORMACAO
1				1	2020-05-15T00:00:00	CASO CONFIRMADO	MASCULINO	0	<1ANO	NAO INFORMADO	NA	NAO INFORMADO	RECUPERADO	NAO INFORMADO	NAO INFORMADO	NAO INFORMADO	2020-08-13T00:00:00	ESUS
2	JUIZ DE FORA	JUIZ DE FORA	SUDESTE	2	2020-05-08T00:00:00	CASO CONFIRMADO	MASCULINO	33	30 A 39 ANOS	JUIZ DE FORA	313670	NAO INFORMADO	RECUPERADO	NAO	NAO	NAO INFORMADO	2020-08-13T00:00:00	ESUS
3	GOVERNADOR VALADARES	GOVERNADOR VALADARES	LESTE	3	2020-06-19T00:00:00	CASO CONFIRMADO	FEMININO	25	20 A 29 ANOS	GOVERNADOR VALADARES	312770	NAO	EM ACOMPANHAMENTO	NAO	NAO	NAO INFORMADO	2020-08-13T00:00:00	ESUS
4				4	2020-06-14T00:00:00	CASO CONFIRMADO	MASCULINO	36	30 A 39 ANOS	NAO INFORMADO	NA	NAO INFORMADO	EM ACOMPANHAMENTO	NAO INFORMADO	NAO INFORMADO	NAO INFORMADO	2020-08-13T00:00:00	ESUS
5	TEOFILO OTONI	TEOFILO OTONI/MALACACHETA	NORDESTE	5	2020-06-14T00:00:00	CASO CONFIRMADO	MASCULINO	51	50 A 59 ANOS	TEOFILO OTONI	316860	NAO INFORMADO	INVESTIGACAO	SIM	NAO	NAO INFORMADO	2020-08-13T00:00:00	SIVEP
6	GOVERNADOR VALADARES	GOVERNADOR VALADARES	LESTE	6	2020-06-05T00:00:00	CASO CONFIRMADO	MASCULINO	41	40 A 49 ANOS	GOVERNADOR VALADARES	312770	NAO	RECUPERADO	NAO	NAO	NAO INFORMADO	2020-08-13T00:00:00	ESUS

covid_MG = covid_MG %>% mutate(INTERNACAO = ifelse(INTERNACAO =="NAO INFORMADO", NA,INTERNACAO),
                               FAIXA_ETARIA = ifelse(FAIXA_ETARIA == "", NA, FAIXA_ETARIA ),
                               SEXO = ifelse(SEXO == "NAO INFORMADO", NA, SEXO ),
                               RACA = ifelse(RACA == "NAO INFORMADO", NA, RACA ),
                               UTI = ifelse(UTI == "NAO INFORMADO", NA, UTI ),
                               COMORBIDADE = ifelse(COMORBIDADE == "NAO INFORMADO", NA, COMORBIDADE))

tabela1<- function(x, y, type.sum){
  t0 <- table(x, y)
  if(type.sum==2) {
    t1 <- prop.table(t0, 2)
  } else {
    t1 <- prop.table(t0, 1)
  }
  colnames(t0) <- paste0("X", 1:dim(t0)[2])
  colnames(t1) <- paste0("X", 1:dim(t1)[2])
  t2_aux <- cbind(t0, t1)
  t3 <- t2_aux[, order(colnames(t2_aux))]
  colnames(t3) <- c(rep(c("N", "%"), dim(t3)[2]/2))
  
  return(t3)
}

Exemplo 1:

Verificar se a proporção de internação é igual no sexo feminino e masculino, ou seja, verificar se as variáveis sexo e internação são independentes.

H₀ : p₁ − p₂ = 0
H₁ : p₁ − p₂ ≠ 0

Aplicação no R

#tabela de contingência com N e %
tabela1(covid_MG$SEXO, covid_MG$INTERNACAO,1)

##               N         %    N         %
## FEMININO  10709 0.6903687 4803 0.3096313
## MASCULINO 12189 0.6852372 5599 0.3147628

tabela <- table(covid_MG$SEXO, covid_MG$INTERNACAO) 
tabela 

##            
##               NAO   SIM
##   FEMININO  10709  4803
##   MASCULINO 12189  5599

#usando a função
prop.test(tabela, conf.level = 0.95, alt="two.sided") #p estimado é proporção de não internações para cada sexo

## 
##  2-sample test for equality of proportions with continuity correction
## 
## data:  tabela
## X-squared = 0.99207, df = 1, p-value = 0.3192
## alternative hypothesis: two.sided
## 95 percent confidence interval:
##  -0.004904591  0.015167607
## sample estimates:
##    prop 1    prop 2 
## 0.6903687 0.6852372

O teste z para duas proporções é equivalente ao teste de independência do qui-quadrado. A função prop.test () calcula formalmente o teste do qui-quadrado. O valor p do teste z para duas proporções é igual ao valor p do teste qui-quadrado e a estatística Z é igual à raiz quadrada da estatística Qui-Quadrado.

Teste Qui-Quadrado

Pressupostos:

• No caso de tabelas 2 × 2, sempre que n ≤ 20 ou as frequências esperadas forem inferiores a 5 deve-se recorrer ao teste exato de Fisher que fornece valores exatos para os p-values do teste.
• Se n > 20 e o número de categorias for maior que 2, não deverá existir mais do que 20% das células com frequências esperadas inferiores a 5 nem deverá existir nenhuma célula com frequência esperada inferior a 1.

Quando temos tabelas 2 × 2, usa-se a correção de Yates quando:

• o valor de Qui Quadrado obtido é maior que o crítico e o valor de N é pequeno;
• o valor de Qui Quadrado obtido é maior que o crítico e há pelo menos uma classe com frequência esperada menor que 5.

A correção é necessária para evitar eventuais conclusões errada, uma vez que quando a amostra ou a frequência esperada é pequena, podemos obter um X² maior do que o valor real.

Qui-Quadrado Independência

O teste Qui-Quadrado de Independência é utilizado para avaliar a associação entre duas variáveis qualitativas X e Y.

OBS: Os totais das colunas e os totais das linhas são aleatórios, ou seja, obtidos por mero acaso.

Hipóteses:

H₀: não há associação entre as variáveis (independentes)
H₁: há associação entre as variáveis (dependentes)

Qui-Quadrado Homogeneidade

O teste qui-quadrado de Homogeneidade é utilizado para avaliar se uma certa característica é homogonênea nos grupos avaliados, ou seja, se a distribuição das frequências é semelhante entre os grupos.

OBS: Os totais das colunas ou das linhas são fixos, ou seja, foram definidos pelo pesquisador.

Hipóteses:

H₀: os grupos são homogêneos
H₁: os grupos não são homogêneos

Estatística de teste:

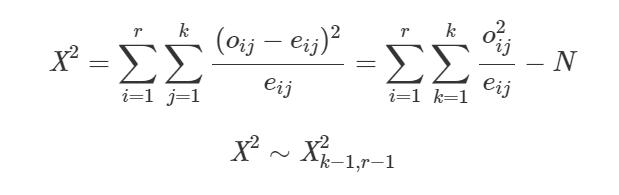
Onde:

• k é o número de colunas
• r é o número de linhas
• o_ij é a frequência observada na linha i, coluna j;
• eij é a frequência esperada na linha i, coluna j;
• e_i= (Total da coluna x Total da linha)/ Total geral

Exemplo 1:

Verificar se há associação entre comorbidades e UTI por covid-19 ao nivel de 5% de significância.

H₀: não há associação entre comorbidades e UTI por covid-19
H₁: há associação entre comorbidades e UTI por covid-19

Aplicação no R

tabela1(covid_MG$COMORBIDADE, covid_MG$UTI,2)

##        N         %    N         %
## NAO 8624 0.6354727  632 0.3370667
## SIM 4947 0.3645273 1243 0.6629333

tabela <- table(covid_MG$COMORBIDADE, covid_MG$UTI)
tabela 

##      
##        NAO  SIM
##   NAO 8624  632
##   SIM 4947 1243

#Calculando os valores esperados 
Ei <- outer(rowSums(tabela), colSums(tabela), "*")/sum(tabela)
chisq.test(tabela)$expected

##      
##            NAO       SIM
##   NAO 8132.408 1123.5919
##   SIM 5438.592  751.4081

#usando a função
chisq.test(tabela, correct = FALSE)

## 
##  Pearson's Chi-squared test
## 
## data:  tabela
## X-squared = 610.84, df = 1, p-value < 2.2e-16

OBS: Quanto temos tabelas com 2 × 2, caso existam frequências esperadas menores que 5, ao utilizar a função chisq.test aparecerá um aviso “A aproximação qui-quadrado pode estar incorreta”. Diante disso, deve-se usar o fisher.test.

Exemplo 2:

Verificar se há associação entre raça e internação por covid-19 ao nivel de 5% de significância.

H₀: não há associação entre raça e internação por covid-19
H₁: há associação entre raça e internação por covid-19

tabela1(covid_MG$RACA, covid_MG$INTERNACAO,1)

##             N         %    N         %
## AMARELA  1668 0.8862912  214 0.1137088
## BRANCA   5802 0.6501569 3122 0.3498431
## INDIGENA   11 0.7857143    3 0.2142857
## PARDA    5838 0.5795691 4235 0.4204309
## PRETA     795 0.5437756  667 0.4562244

tabela <- table(covid_MG$RACA, covid_MG$INTERNACAO)
tabela 

##           
##             NAO  SIM
##   AMARELA  1668  214
##   BRANCA   5802 3122
##   INDIGENA   11    3
##   PARDA    5838 4235
##   PRETA     795  667

#Calculando os valores esperados 
Ei <- outer(rowSums(tabela), colSums(tabela), "*")/sum(tabela)  
chisq.test(tabela)$expected

##           
##                    NAO         SIM
##   AMARELA  1188.215075  693.784925
##   BRANCA   5634.235563 3289.764437
##   INDIGENA    8.839007    5.160993
##   PARDA    6359.665489 3713.334511
##   PRETA     923.044867  538.955133

#usando a função
chisq.test(tabela, correct = FALSE)

## 
##  Pearson's Chi-squared test
## 
## data:  tabela
## X-squared = 704.77, df = 4, p-value < 2.2e-16

Exemplo 3:

Verificar se os grupos são homogêneos com relação ao IMC, ao nível de 5% de significância.

H₀: os grupos são homogêneos.
H₁: os grupos não são homogêneos.

dados <- read.csv2("Dados.csv")
head(dados)

##   ID Idade      Sexo     Classificação.IMC Diabetes Grupo
## 1  1    63 Masculino Adequado ou Eutrófico      Sim  GAVC
## 2  2    63 Masculino            Baixo peso      Sim  GAVC
## 3  3    70  Feminino            Baixo peso      Sim  GAVC
## 4  4    73 Masculino Adequado ou Eutrófico      Não  GAVC
## 5  5    71 Masculino             Sobrepeso      Não  GAVC
## 6  6    60 Masculino            Baixo peso      Sim  GAVC

tabela1(dados$Classificação.IMC, dados$Grupo,2)

##                        N     %  N     %
## Adequado ou Eutrófico 19 0.475 17 0.425
## Baixo peso            12 0.300  4 0.100
## Sobrepeso              9 0.225 19 0.475

tabela <- table(dados$Classificação.IMC, dados$Grupo)
tabela 

##                        
##                         GAVC GC
##   Adequado ou Eutrófico   19 17
##   Baixo peso              12  4
##   Sobrepeso                9 19

#Calculando os valores esperados 
Ei <- outer(rowSums(tabela), colSums(tabela), "*")/sum(tabela)  
chisq.test(tabela)$expected

##                        
##                         GAVC GC
##   Adequado ou Eutrófico   18 18
##   Baixo peso               8  8
##   Sobrepeso               14 14

#usando a função
chisq.test(tabela)

## 
##  Pearson's Chi-squared test
## 
## data:  tabela
## X-squared = 7.6825, df = 2, p-value = 0.02147

OBS: Quanto temos tabelas com variáveis com categorias > 2 e existir mais do que 20% das células com frequências esperadas inferiores a 5 ou alguma célula teve frequência esperada inferior a 1, deve-se utilizar o argumento simulate.p.value = TRUE, para que o valor-p seja calculado através da simulação de Monte Carlo.

Amostras dependentes

Em amostras emparelhadas ou dependentes os elementos das amostras provém dos mesmos indivíduos ou de indivíduos pareados (em pares) que são muito semelhantes (exemplo: gêmeos).

Teste de McNemar

O teste de McNemar é aplicável aos experimentos do tipo “antes e depois” em que cada indivíduo é seu próprio controle, ou seja, cada indivíduo é observado duas vezes: antes e depois de um certo tratamento e deseja-se testar a significância de mudanças ocorridas de uma categoria para outra são aleatórias ou não.

Assim, temos que “B” indivíduos mudaram da categoria – para a + e “C” indivíduos mudaram de + para -. Portanto, “B+C” é o número total de pessoas que mudaram de resposta e a frequência esperada em cada uma das células é (B+C)/2.

A fórmula do teste de Mc Nemar se origina da fórmula do Qui-quadrado. Porém, são utlizadas as células de interesse (B e C).

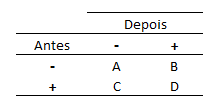
Estatística de teste:

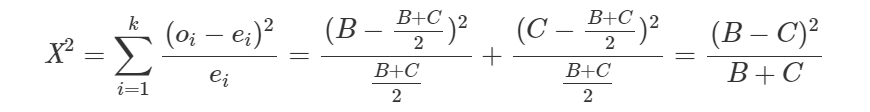
Nesse caso também é importante fazer uma correção de continuidade, pois estamos aproximando uma distribuição contínua, no caso, Qui-Quadrado a uma distribuição discreta. Além disso, quando todas as freqüências esperadas são pequenas, está aproximação pode não ser boa. Logo, a correção de continuidade (de Yates) é uma tentativa de remover esta fonte de erro.

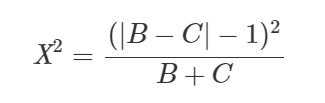
• A hipótese nula é de que o número de mudanças em cada direção é igualmente provável (aleatória), isto é, dos “b+c” indivíduos que mudaram, espera-se que (b+c)/2 mudassem de + para – e (b+c)/2 mudassem de – para +.

Hipótese:

H₀ : P(+antes, −depois) = P(−antes, +depois)
H₁ : C.C

Ou

H₀: Não existe diferença entre antes e depois
H₁: Existe diferença entre antes e depois

Exemplo:

Dois supermercados disputam a preferência dos consumidores de uma cidade do interior. O supermercado A realiza então uma campanha com distribuição de prêmios para aumentar o número de clientes. 85 consumidores foram acompanhados antes e depois da campanha, onde perguntou-se a cada um deles sobre a sua preferência de supermercado.

H₀: não existe diferença entre antes e depois da ação do supermercado A
H₁: existe diferença entre antes e depois da ação do supermercado A

Aplicação no R

supermercados <- matrix(c(32, 13, 3, 37), nrow = 2,
                      dimnames = list("Antes" = c("A", "B"),
                                      "Depois" = c("A", "B")))
supermercados

##      Depois
## Antes  A  B
##     A 32  3
##     B 13 37

mcnemar.test(supermercados, correct = TRUE)

## 
##  McNemar's Chi-squared test with continuity correction
## 
## data:  supermercados
## McNemar's chi-squared = 5.0625, df = 1, p-value = 0.02445

k amostras

Amostras independentes

Qui-Quadrado

Pressupostos:

• No máximo 20% das células tenham frequências esperadas < 5 e todas as células tenham frequências esperadas > 1. (Conservador)

Hipóteses:

H₀: os k grupos são homogêneos.
H₁: pelo menos um grupo é diferente.

Estatística de teste:

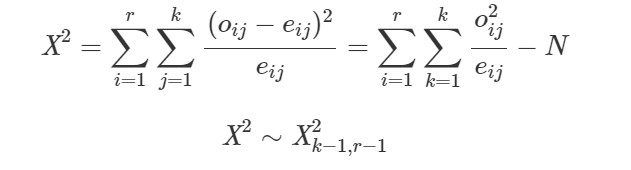
Exemplo

Verificar se existe diferença de classificação do IMC entre o sexo feminino e masculino, ou seja, verificar se as variáveis sexo e IMC são independentes.

H₀: as classificações do IMC são homogêneas entre os sexos.
H₁: pelo menos uma classificação é diferente entre os sexos.

Aplicação no R

tabela1(dados$Sexo, dados$Classificação.IMC,1)

##            N         %  N          %  N         %
## Feminino  15 0.4166667  3 0.08333333 18 0.5000000
## Masculino 21 0.4772727 13 0.29545455 10 0.2272727

tabela <- table(dados$Sexo, dados$Classificação.IMC)
tabela 

##            
##             Adequado ou Eutrófico Baixo peso Sobrepeso
##   Feminino                     15          3        18
##   Masculino                    21         13        10

#Calculando os valores esperados 
Ei <- outer(rowSums(tabela), colSums(tabela), "*")/sum(tabela)  
chisq.test(tabela)$expected

##            
##             Adequado ou Eutrófico Baixo peso Sobrepeso
##   Feminino                   16.2        7.2      12.6
##   Masculino                  19.8        8.8      15.4

#usando a função
chisq.test(tabela)

## 
##  Pearson's Chi-squared test
## 
## data:  tabela
## X-squared = 8.824, df = 2, p-value = 0.01213

Amostras dependentes

Teste Q de Cochran

O Teste Q de Cochran é uma extensão do teste de McNemar para mais de duas amostras. Assim ele testa se três ou mais tratamentos combinados diferem significativamente entre si, considerando proporção ou frequência.

Devemos considerar k tratamentos (colunas) e r individuos/unidades (linhas). Onde os r indivíduos são observados em três ou mais tratamentos(etapas)

Os resultados são representados de forma dicotômica: podendo ser 1(sucesso) ou 0(fracasso), com o intuito de verificar se a frequência de respostas 1 ou 0 é a mesma em cada tratamento (coluna).

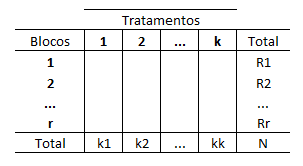
Estatística de teste:

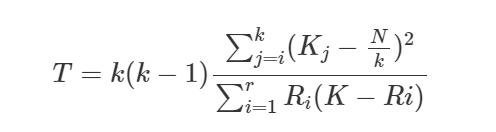
Como a distribuição T é difícil de ser calculada usa-se uma aproximação pela distribuição Qui-Quadrado com K-1 graus de liberdade.

Hipótese:

H₀: a frequência é a mesma nos k tratamentos
H₁: existe pelo menos uma diferença entre dois tratamentos

Quando há evidências para rejeitar a H₀, pode-se usar o teste de Mc Nemar para fazer comparações múltiplas.

Exemplo: Um entrevistador enviou 3 formulários para 10 indivíduos sobre a preferência de cada um sobre um produto comercial lançado recentemente, sendo que um cada formulário foi enviado com intervalo de 1 mês entre cada um. o entrevistador avaliou os formulários e quando o individuo ficou satisfeito ele recebeu 1 e quando não ficou satisfeito recebeu 0.

H₀: a frequência de ser satisfeito é igual em todos os três formulários.
H₁: existe pelo menos uma diferença entre dois formulários.

Aplicação no R

satisfacao <- data.frame(ID = c(1,2,3,4,5,6,7,8,9,10),
                         F1 = c(1,0,0,0,1,0,1,0,0,1),
                         F2 = c(0,1,1,1,1,0,0,0,1,0),
                         F3 = c(1,0,0,1,0,0,1,0,0,0))
satisfacao

##    ID F1 F2 F3
## 1   1  1  0  1
## 2   2  0  1  0
## 3   3  0  1  0
## 4   4  0  1  1
## 5   5  1  1  0
## 6   6  0  0  0
## 7   7  1  0  1
## 8   8  0  0  0
## 9   9  0  1  0
## 10 10  1  0  0

if(!require(nonpar)){install.packages("nonpar");require(nonpar)}

dados_st <- cbind(satisfacao$F1,satisfacao$F2, satisfacao$F3) 
cochrans.q(dados_st)

## 
##  Cochran's Q Test 
##  
##  H0: There is no difference in the effectiveness of treatments. 
##  HA: There is a difference in the effectiveness of treatments. 
##  
##  Q = 0.75 
##  
##  Degrees of Freedom = 2 
##  
##  Significance Level = 0.05 
##  The p-value is  0.687289278790972 
##   
##