Artigo desenvolvido com a colaboração de Luana Sílvia dos Santos
Hoje, apresentaremos um exemplo prático de modelagem de equações estruturais via PLS (Partial Least Squares).
O exemplo utilizará o banco de dados spainfoot do pacote plspm do software R. O banco de dados é composto por 12 variáveis medidas em 20 times da liga espanhola de futebol (La Liga) no período de 2008 a 2009.
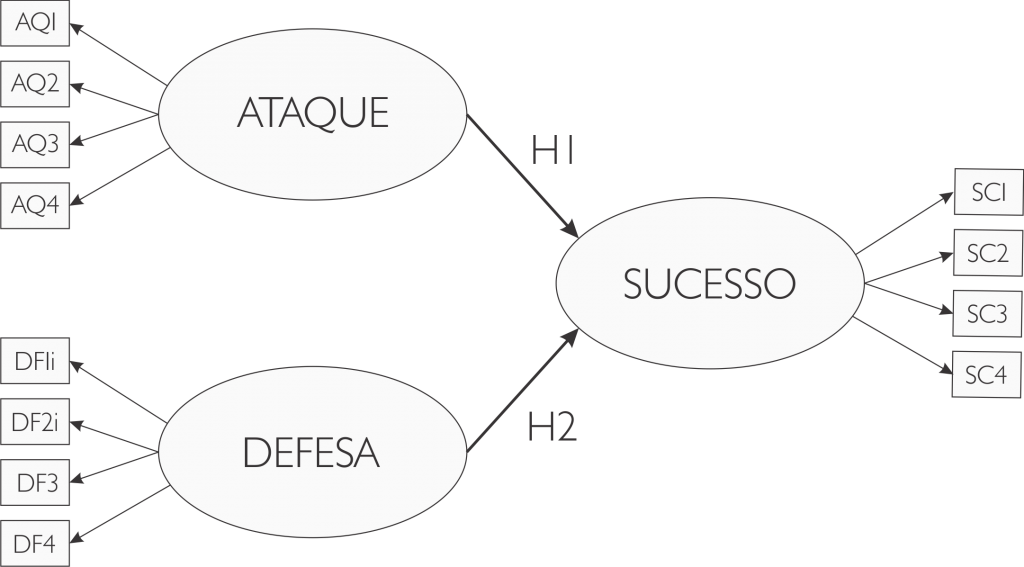
Defesa, Ataque e o Sucesso do Time
Nosso interesse aqui é verificar a relação entre defesa e o sucesso do time e ataque e o sucesso do time. Sendo assim, testaremos duas hipóteses:
- H1: Quanto melhor o Ataque do time, maior tende a ser o Sucesso.
- H2: Quanto melhor a Defesa do time, maior tende a ser o Sucesso.
Por esse motivo, formaremos as variáveis Ataque, Defesa e Sucesso uma vez que, na condição de variáveis latentes, não são medidas diretamente, mas através de outros indicadores. A seguir listamos os indicadores que formarão cada um desses constructos.
| Constructo | Questão | Descrição |
| Ataque | AQ1 | Número de gols marcados em casa |
| AQ2 | Número de gols marcados fora | |
| AQ3 | Percentual de jogos com gols marcados em casa | |
| AQ4 | Percentual de jogos com gols marcados fora | |
| Defesa | DF1 | Número de golos concedidos em casa |
| DF2 | Número de gols concedidos fora | |
| DF3 | Percentual de jogos sem gols concedidos em casa | |
| DF4 | Percentual de jogos sem gols concedidos fora | |
| Sucesso | SC1 | Número de jogos vencidos em casa |
| SC2 | Número de jogos vencidos fora | |
| SC3 | Maior sequência de vitorias (nº de jogos) | |
| SC4 | Maior sequência de invencibilidade (nº de jogos) |
Ao observar a tabela acima podemos verificar que os itens DF1 e DF2 estão invertidos, ou seja, eles se encontram em um sentido diferente dos demais do constructo, de forma que quanto maior forem esses itens, menor será a defesa.
Sendo assim, é necessário que esses itens sejam invertidos para que quanto maior os seus valores, maior seja defesa. Isso pode ser feito multiplicando os itens por -1, mas deve-se estar atento para inserir a letra “i” na frente dos mesmos quando forem mencionados, para identificar a inversão realizada.
Vamos então carregar a base de dados e criar nossas variáveis e constructos no R.
# Carregando a base de dados e visualizando o cabeçalho com cinco itens amostrais > data(spainfoot) > head(spainfoot, n = 5) GSH GSA SSH SSA GCH GCA CSH CSA WMH WMA LWR LRWL YC RC Barcelona 61 44 0.95 0.95 14 21 0.47 0.32 14 13 10 22 76 6 RealMadrid 49 34 1.00 0.84 29 23 0.37 0.37 14 11 10 18 115 9 Sevilla 28 26 0.74 0.74 20 19 0.42 0.53 11 10 4 7 100 8 AtleMadrid 47 33 0.95 0.84 23 34 0.37 0.16 13 7 6 9 116 5 Villarreal 33 28 0.84 0.68 25 29 0.26 0.16 12 6 5 11 102 5 # Definindo as variáveis > AQ1<- spainfoot$GSH > AQ2<- spainfoot$GSA > AQ3<- spainfoot$SSH > AQ4<- spainfoot$SSA > DF1i<- spainfoot$GCH*-1 > DF2i<- spainfoot$GCA*-1 > DF3<- spainfoot$CSH > DF4<- spainfoot$CSA > SC1<- spainfoot$WMH > SC2<- spainfoot$WMA > SC3<- spainfoot$LWR > SC4<- spainfoot$LRWL # Definindo os constructos > AQ<- cbind(AQ1, AQ2, AQ3, AQ4) > DF<- cbind(DF1i, DF2i, DF3, DF4) > SC<- cbind(SC1, SC2, SC3, SC4)
O modelo de equações estruturais
Tendo as informações de quais indicadores fazem parte de quais constructos, quais perguntas estão invertidas, quais hipóteses devem ser testadas e assumindo que os constructos em questão são todos reflexivos, é possível representar o modelo de equações estruturais da seguinte forma:
Método Utilizado: PLS
O modelo de mensuração e modelo de regressão foram ajustados utilizando o método PLS (Partial Least Square). Modelos de Equações Estruturais (SEM) são muito populares em muitas disciplinas, sendo a abordagem PLS (Partial Least Square) uma alternativa a abordagem tradicional baseada na covariância.
A abordagem PLS tem sido referida como uma técnica de modelagem suave com o mínimo de demanda, ao se considerar as escalas de medidas, o tamanho amostral e distribuições residuais (Monecke, et al., 2012).
Vamos então ajustar o modelo de equações estruturais no R, utilizando o método PLS:
> data<- data.frame(AQ, DF, SC)
> Attack = c(0, 0, 0)
> Defense = c(0, 0, 0)
> Success = c(1, 1, 0)
> foot_path = rbind(Attack, Defense, Success)
> colnames(foot_path) = rownames(foot_path)
> foot_blocks = list(1:4, 5:8, 9:12)
> foot_modes = c("A", "A", "A")
> foot_pls = plspm(data, foot_path, foot_blocks, modes = foot_modes)
> summary(foot_pls)
PARTIAL LEAST SQUARES PATH MODELING (PLS-PM)
----------------------------------------------------------
MODEL SPECIFICATION
1 Number of Cases 20
2 Latent Variables 3
3 Manifest Variables 12
4 Scale of Data Standardized Data
5 Non-Metric PLS FALSE
6 Weighting Scheme centroid
7 Tolerance Crit 1e-06
8 Max Num Iters 100
9 Convergence Iters 4
10 Bootstrapping FALSE
11 Bootstrap samples NULL
----------------------------------------------------------
BLOCKS DEFINITION
Block Type Size Mode
1 Attack Exogenous 4 A
2 Defense Exogenous 4 A
3 Success Endogenous 4 A
----------------------------------------------------------
BLOCKS UNIDIMENSIONALITY
Mode MVs C.alpha DG.rho eig.1st eig.2nd
Attack A 4 0.891 0.925 3.02 0.792
Defense A 4 0.772 0.855 2.39 1.175
Success A 4 0.917 0.942 3.22 0.537
----------------------------------------------------------
OUTER MODEL
weight loading communality redundancy
Attack
1 AQ1 0.337 0.938 0.880 0.000
1 AQ2 0.282 0.862 0.743 0.000
1 AQ3 0.289 0.841 0.707 0.000
1 AQ4 0.240 0.826 0.683 0.000
Defense
2 DF1i 0.109 0.484 0.234 0.000
2 DF2i 0.391 0.876 0.767 0.000
2 DF3 0.327 0.746 0.557 0.000
2 DF4 0.404 0.893 0.797 0.000
Success
3 SC1 0.231 0.776 0.601 0.515
3 SC2 0.303 0.886 0.786 0.672
3 SC3 0.282 0.969 0.938 0.803
3 SC4 0.296 0.944 0.891 0.762
----------------------------------------------------------
CROSSLOADINGS
Attack Defense Success
Attack
1 AQ1 0.938 0.516 0.898
1 AQ2 0.862 0.339 0.752
1 AQ3 0.841 0.414 0.771
1 AQ4 0.826 0.336 0.639
Defense
2 DF1i 0.131 0.484 0.160
2 DF2i 0.462 0.876 0.575
2 DF3 0.319 0.746 0.481
2 DF4 0.421 0.893 0.593
Success
3 SC1 0.709 0.423 0.776
3 SC2 0.773 0.711 0.886
3 SC3 0.844 0.538 0.969
3 SC4 0.860 0.589 0.944
----------------------------------------------------------
INNER MODEL
$Success
Estimate Std. Error t value Pr(>|t|)
Intercept -3.05e-17 0.0922 -3.31e-16 1.00e+00
Attack 7.57e-01 0.1044 7.25e+00 1.35e-06
Defense 2.84e-01 0.1044 2.72e+00 1.47e-02
----------------------------------------------------------
CORRELATIONS BETWEEN LVs
Attack Defense Success
Attack 1.00 0.470 0.890
Defense 0.47 1.000 0.639
Success 0.89 0.639 1.000
----------------------------------------------------------
SUMMARY INNER MODEL
Type R2 Block_Communality Mean_Redundancy AVE
Attack Exogenous 0.000 0.753 0.000 0.753
Defense Exogenous 0.000 0.589 0.000 0.589
Success Endogenous 0.856 0.804 0.688 0.804
----------------------------------------------------------
GOODNESS-OF-FIT
[1] 0.7823
----------------------------------------------------------
TOTAL EFFECTS
relationships direct indirect total
1 Attack -> Defense 0.000 0 0.000
2 Attack -> Success 0.757 0 0.757
3 Defense -> Success 0.284 0 0.284
Modelo de Mensuração
No modelo de mensuração de constructos reflexivos são verificadas a validade convergente, a validade discriminante, a confiabilidade e a dimensionalidade dos construtos. Mais detalhes sobre a validação podem ser vistos no artigo sobre a validação do modelo de mensuração.
A tabela abaixo resume o modelo de mensuração. A partir dela pode-se verificar que todos os itens apresentaram cargas fatoriais e pesos altos, indicando que eles contribuem de forma relevante para a formação da variável latente.
| Constructos | Itens | Peso | Carga Fatorial | Comunalidade |
| Ataque | AQ1 | 0,337 | 0,938 | 0,880 |
| AQ2 | 0,282 | 0,862 | 0,743 | |
| AQ3 | 0,289 | 0,841 | 0,707 | |
| AQ4 | 0,240 | 0,826 | 0,683 | |
| Defesa | DF1i | 0,109 | 0,484 | 0,234 |
| DF2i | 0,391 | 0,876 | 0,767 | |
| DF3 | 0,327 | 0,746 | 0,557 | |
| DF4 | 0,404 | 0,893 | 0,797 | |
| Sucesso | SC1 | 0,231 | 0,776 | 0,601 |
| SC2 | 0,303 | 0,886 | 0,786 | |
| SC3 | 0,282 | 0,969 | 0,938 | |
| SC4 | 0,296 | 0,944 | 0,891 |
Com os resultados da análise da validade convergente, a validade discriminante, dimensionalidade e a confiabilidade dos construtos, pode-se destacar que:
- todos os constructos apresentaram os índices de confiabilidade Alfa de Cronbach ou Confiabilidade Composta acima de 0,70, evidenciando assim a confiabilidade dos constructos;
- todos os constructos foram unidimensionais pelo critério de retas paralelas;
- todos os constructos apresentaram variância extraída superior a 0,50, indicando validação convergente.
De acordo com o critério proposto por Fornell e Larcker (1981) não houve validação discriminante para os constructos, uma vez que suas maiores variâncias compartilhadas foram maiores que suas respectivas variâncias extraídas.
| Constructos | Ataque | Defesa | Sucesso |
| Alfa de Cronbach | 0,891 | 0,772 | 0,917 |
| Confiabilidade Composta | 0,925 | 0,855 | 0,942 |
| Dimensionalidade | 1 | 1 | 1 |
| Variância Extraída | 0,753 | 0,589 | 0,804 |
| Máximo da Variância Compartilhada | 0,792 | 0,408 | 0,792 |
Observamos que, a partir do critério proposto por Fornell e Larcker, não foi possível ter a validação discriminante dos constructos. Nesse caso, podemos utilizar o método das cargas fatoriais cruzadas (Barclay et al.,1995). Nele, o critério de validação discriminante é alcançado quando as cargas fatoriais dos itens forem maiores que todas suas maiores cargas fatoriais cruzadas.
| Constructos | Itens | Carga Fatorial | Máximo da Carga Fatorial Cruzada |
| Ataque | AQ1 | 0,938 | 0,898 |
| AQ2 | 0,862 | 0,752 | |
| AQ3 | 0,841 | 0,771 | |
| AQ4 | 0,826 | 0,639 | |
| Defesa | DF1i | 0,484 | 0,160 |
| DF2i | 0,876 | 0,575 | |
| DF3 | 0,746 | 0,481 | |
| DF4 | 0,893 | 0,593 | |
| Sucesso | SC1 | 0,776 | 0,709 |
| SC2 | 0,886 | 0,773 | |
| SC3 | 0,969 | 0,844 | |
| SC4 | 0,944 | 0,860 |
Como todas as cargas fatoriais dos itens foram maiores que todas suas maiores cargas fatoriais cruzadas, se pode verificar a validação discriminante dos constructos.
Agora que verificamos a validade convergente, a validade discriminante, dimensionalidade e a confiabilidade dos construtos, passamos a avaliar o modelo estrutural.
Modelo Estrutural
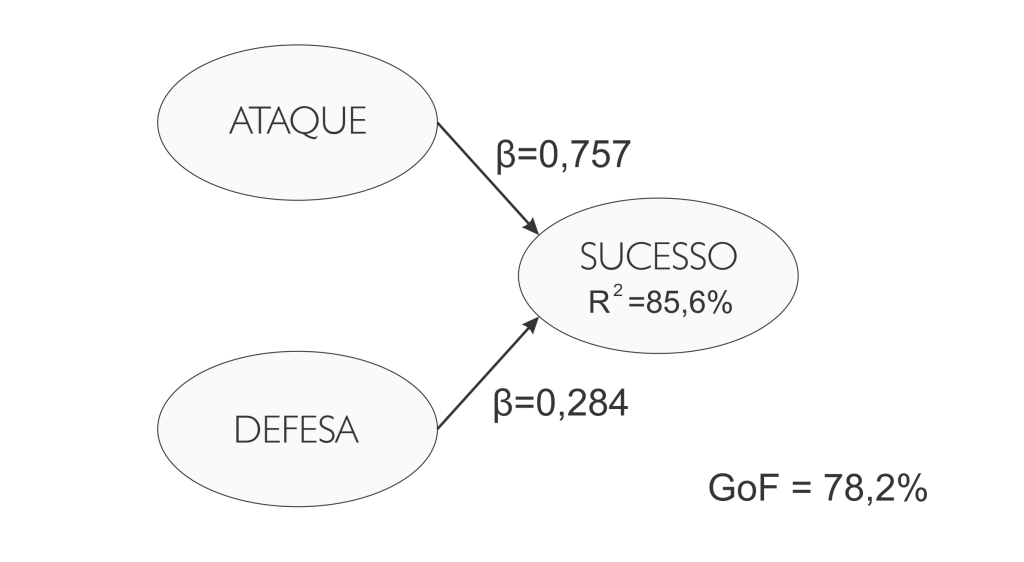
A tabela abaixo apresenta o resultado do modelo estrutural, onde pode-se verificar que houve influência significativa e positiva do ataque sobre o sucesso, sendo que quanto maior o ataque, maior tende a ser o sucesso. Também houve influência significativa da defesa sobre o sucesso, sendo que quanto maior a defesa, maior tende a ser o sucesso.
| Endógena | Exógenas | β | E.P. (β)¹ | Valor-p |
| Sucesso | Ataque | 0,757 | 0,104 | 0,000 |
| Defesa | 0,284 | 0,104 | 0,015 | |
| ¹ Erro Padrão; R² = 85,6%; GoF = 78,2%. | ||||
Para verificar a qualidade dos ajustes foram utilizados o R2 e o GoF (Tenenhaus, et al., 2004). O R2 representa em uma escala de 0% a 100% o quanto os constructos independentes explicam os dependentes.
Já o GoF é uma média geométrica das AVEs dos construtos e dos R² do modelo e também varia de 0% a 100%. O GoF em PLS não tem a capacidade de discriminar modelos válidos de inválidos, além de não se aplicar para modelos com constructos formativos (Henseler and Sarstedt, 2012). Nesses casos ele apenas permite uma síntese das AVEs e dos R² do modelo em uma única estatística, podendo ser útil para futuras comparações de aderência de diferentes amostras ao modelo.
Observamos que o ataque e a defesa conseguiram explicar 85,6% da variabilidade do sucesso. Além disso, o modelo apresentou um GoF de 78,2%.
Esse foi apenas um exemplo de aplicação da técnica de modelagem de equações estruturais. Como já dissemos, é uma técnica muito utilizada e as interpretações e análises que podem surgir de um modelo estrutural contribuem muito para o entendimento dos fenômenos estudados.