Modelo Linear Misto

Artigo escrito com a colaboração de Alice Ferreira

O principal objetivo do modelo linear misto é remover a premissa de independência dos dados, da análise de regressão comum. Por exemplo, se desejamos prever o volume de vendas de vendedores e esses pertencem a regiões diferentes e a organizações de vendas diferentes, fica evidente que as variáveis possuem uma hierarquia, ou seja, são dependentes.

Como tratar dados hierárquicos?

Como eles quebram a premissa de independência, não podemos seguir com uma regressão linear usual, então o que fazer?

Resumir os dados:
Uma abordagem simples é resumir os dados, no exemplo acima iríamos pegar as regiões, que são o nível máximo, e utilizar a média por grupo no lugar das observações individuais. Dessa maneira os dados seriam independentes.

Porém você já deve imaginar que essa abordagem não é a ideal, pois muitas vezes teríamos um número de observações como o do exemplo acima, n = 4.

Separar os dados:
Outra abordagem seria realizar uma modelagem por região, separando nossos dados em 4 bancos diferentes e aplicando 4 modelos, um por banco. Porém isso também gera perda de informação sobre a regionalidade, sobre a dispersão entre regiões.

Isso também gera modelos baseados em menos dados, tornando eles menos assertivos.

A regressão linear de modelos mistos pode ser vista como um intermédio entre essas propostas.

Vantagens do LMER

Não possui premissa de independência entre as variáveis explicativas

A variável dependente pode ser categórica, ordinal ou discreta!

A variável tempo é contínua.
Na ANOVA a variável de tempo é categórica, isso torna o modelo LMER mais vantajoso! Por exemplo, se tivermos os meses 1,2,3, e 5, a ANOVA as entende como categorias, já o LMER identifica essa diferença de dispersão.

Fatores fixos e aleatórios

O principal objetivo do modelo linear misto é remover a premissa de independência dos dados, permitindo que tenhamos tanto efeitos fixos quanto efeito aleatório.

Diferença teórica

Os fatores fixos são paramétricos que não variam, igual aos dos tradicionais modelos de regressão. Assumimos que há um valor verdadeiro de β o tentamos estimar, ele é parâmetro desconhecido.

Já os fatores aleatórios são variáveis aleatórias, por exemplo, poderíamos dizer que um parâmetro β com média μ e variância σ tem a distribuição:

Podemos observar os fatores aleatórios como parte de uma população maior do que a amostrada, ou seja, uma VA. No modelo de efeitos mistos não atentamos a cada nível dos fatores aleatórios, não importamos com cada fator, o importante é que possuem uma sequência de fatores e queremos levar em conta sua variabilidade.

Então a regressão linear pode ser vista como um modelo linear de efeitos mistos mas com apenas fatores fixos. Agora, como identificar esses fatores? Não há uma regra, isso irá depender da sua variável resposta e do seu banco de dados. Mas há algumas diretrizes que podemos seguir.

Fatores Fixos: são os fatores que você esta mais interessado, aqueles que tem mais importância sob o modelo.

Fatores aleatórios: Os fatores randômico normalmente são as que você não se importa tanto com a variável em si, mas deseja levar em conta no modelo diferenças potenciais entre os grupos, ou seja, levar em conta a variância.

Diferença prática

Os modelos lineares de efeitos mistos usam algo chamado “restricted maximum likelihood estimation” (REML) para modelar esses efeitos aleatórios, e seus resíduos (que no exemplo abaixo seriam a diferença entre os pontos e as linhas).

Porém como o fator vem de uma VA , o modelo estima um intercepto e/ou inclinação para cada categoria. Isso pode ter um poder muito significativo para nossa análise, como mostrado abaixo:

Sem a análise da variância das categorias acreditamos que as variáveis ‘Salário’ e ‘Neuroticismo’ possui uma correlação diretamente proporcional, mas através da análise do efeito aleatório escolaridade, observamos que possuem uma relação inversamente proporcional.

Os fatores vem de uma variável aleatória desconhecida ->
Estimamos os melhores fatores para cada categoria da variável ->
Como vem de uma VA, os estimadores podem diferir.

Tratamento para fatores aleatórios

Uma opção, mostrada na primeira imagem, é partimos da premissa que os fatores aleatórios possuem interceptos diferentes, mas possuem mesma inclinação. Fórmula:

Também poderíamos partir do inverso, de que os interceptos são iguais porém a inclinação difere.

Ou ainda, seguir da premissa de que tanto o intercepto quanto a inclinação podem diferir, como mostrado na segunda imagem. Fórmula:

Tipos de efeitos aleatórios

Lembrando que os fatores aleatórios vêm de uma variável categórica independente e desconhecida, e para o método estimar essa distribuição precisamos de muitas estimativas.

Essas estimativas são calculas por cada grupo da variável, como mostrado acima, então os os efeitos aleatórios devem ter muitas categorias! Normalmente dizemos que menos de 5 grupos é sugerido que os tratem como efeitos fixos.

O método precisa estimar a distribuição das categorias dos efeitos aleatórios, se tivermos apenas 4 categorias fica muito difícil estimar esse tipo de VA de maneira adequada.

Nested Effects

• Os Efeitos Aninhados são aqueles que possuem categorias únicas, não possuindo níveis iguais para categorias de hirar superior.
• Na imagem acima poderíamos considerar os números em vermelhos os vendedores e as caixas pontilhadas seus gerentes, eles são Nasted Effects, pois os números não cruzam entre caixas.

Outro exemplo:

Crossed Efects

Os crossed effects são os que possuem todas suas opções de cetegórias nas hierarquia superior, como mostrado na imagem acima, em que a sombra esverdeada e a sombra azulada apercem em todas as caixas pontilhadas.

Fazendo um paralelo com os exemplos anteriores essas sombras poderiam ser tipos de materias que os gerentes venderam, como materiais refrigerados ou não.

Esse exemplo é de um efeito cruzado inteiro, pois as duas cores ocorrem em todas as caixas, se isso não ocorrer ainda o chamaria de efeito cruzado mas não inteiro.

Outro exemplo:

Na prática, os efeitos cruzados são aqueles que não são aninhados.

Aplicando o modelo misto

Pacotes

Ao baixar o pacote lmer4 é indicado que seja instalado uma versão antiga dele, isso irá evitar problemas ao extrair os coeficientes de efeitos aleatórios de bancos de dados grandes.

# InstallOldPackages("lme4", versions = "1.1-15")
# install.packages('JWileymisc')
library(lme4)
library(lmerTest)
library(haven)
library(tidyverse)

O banco de dados usado contém cerca de 2 mil alunos de determinada escola, com suas respectivas classes, grau de extroversão, sexo, anos de experiência de seu professor e grau de popularidade.

popular2data <- read_sav(file = "popular2.sav") %>% 
  select(pupil, class, extrav, sex, texp, popular)

popular2data %>% head()

## # A tibble: 6 x 6
##   pupil class extrav       sex  texp popular
##   <dbl> <dbl>  <dbl> <dbl+lbl> <dbl>   <dbl>
## 1     1     1      5  1 [girl]    24     6.3
## 2     2     1      7  0 [boy]     24     4.9
## 3     3     1      4  1 [girl]    24     5.3
## 4     4     1      3  1 [girl]    24     4.7
## 5     5     1      5  1 [girl]    24     6  
## 6     6     1      4  0 [boy]     24     4.7

• pupil: aluno
• class: turma
• extrav: grau de extroversão
• sex: sexo
• texp: anos de experiência do seu professor
• popular: grau de popularidade

Para evitar os problemas de sobreajuste, Barr et al. (2013) sugerem que comecemos a análise da maneira com a estrutura mais complexa possível para os efeitos aleatórios. Caso o modelo tenha problemas de sobreajuste ou de convergência no método iterativo, devemos simplificar esta estrutura até atingir uma convergência sem problemas.

Porém isso é algo relativo, pois depende da quantidade de variáveis ou complexidade do seu banco de dados. Neste caso, como possuímos poucas iremos seguir essa lógica!

Análise das variáveis

Antes de iniciar a análise vamos observar as relações das variáveis de interesse com a variável resposta desejada: popular

Podemos observar que no geral a popularidade tem uma relação positiva com a extroversão, o que faz sentido! Agora vamos considerar as 100 classes.

• O gráfico a princípio pode parecer confuso, mas nos modelos mistos como os efeitos aleatórios são tratados como uma variável aleatória esperamos que eles possuam muitas categorias, pois assim temos uma amostra maior dos interceptos e inclinações!
• Se analisarmos de maneira geral continuamos observando uma relação positiva entre as variáveis (inclinação positiva) para maioria das classes, e com uma diferença significativa nos interceptos! Segue que é razoável assumir que cada classe tem uma influência de diferente sobre a popularidade do aluno, afetando a distribuição dos dados.
• Isso significa que cada classe contribui com uma variabilidade aleatória que deve ser prevista no modelo. E como possui um número de categorias sufuciente, devemos considerar a variável classe como um efeito aleatório.

• Aqui estamos determinando que o modelo considere interceptos diferentes para cada classe (o número 1, aqui, representa o intercepto). Esse intercepto é chamado de intercepto aleatório, visto que ele tem por objetivo modelar um fator de variabilidade aleatória: as classes (nós podemos chamar esse intercepto específico de intercepto aleatório por classe).

• Podemos observar que a variável sexo possui inclinações muito similares, diferindo apenas nos interceptos.
• Como o número de categorias é ínfimo,  não podemos considerar a variável como um efeito aleatório, além disso não podemos afirmar que ele influência de maneira diferente sobre a popularidade do aluno, pois suas inclinações são similares.

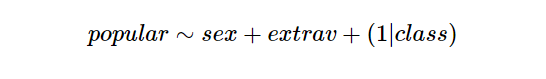
• Além disso devemos adicionar a variável numérica dos anos de experiência dos professores, que como é uma variável numerica deve ser tratada como um fator fixo, e também desejamos acionar um intercepto para o modelo, resultando na seguinte fórmula:

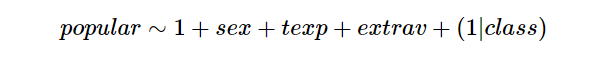
Slope Aleatório!

• Porém como visto anteriormente possuimos várias maneiras de lidarmos com os efeitos aleatórios, e o ideal neste caso é a que a classe possua interceptos e inclinações diferentes para cada categoria! Ou seja, possuam também slopes aleatórios (inclinações)!

• A fórmula aplicada acima (1|class)(1|class) se refere a que possui apenas interceptos diferentes

• Como desejamos que a inclinação da classe seja alterada para cada categoria de cada variável categórica (partindo do modelo mais complexo) devemos usar a fórmula:

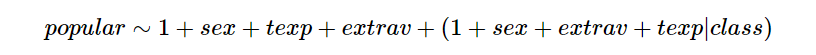
O que a sintaxe (1 + sex + extrav + texp|class)(1 + sex + extrav + texp|class) indica é:

“intercepto aleatório +
slope aleatório por sexo por classe +
slope aleatório por grau de extroversão por classe +
slope aleatório por experiência do professor”.

• Porém é de se imaginar que multiplo splopes vão causar um overfit, logo antes de prosseguirmos vamos analisar os níveis de significante desses slopes! Para isso usamos a função ranova() do pacote lmerTest, pois o summary tradicional não fornece essas informações sobre os efeitos aleatórios.

model <- lmer(formula = popular ~ 1 + sex + extrav + texp + (1 + sex + extrav + texp| class),
               data    = popular2data)

ranova(model)

## ANOVA-like table for random-effects: Single term deletions
## 
## Model:
## popular ~ sex + extrav + texp + (1 + sex + extrav + texp | class)
##                                             npar  logLik    AIC    LRT Df
## <none>                                        15 -2416.6 4863.2          
## sex in (1 + sex + extrav + texp | class)      11 -2417.3 4856.6  1.419  4
## extrav in (1 + sex + extrav + texp | class)   11 -2441.7 4905.4 50.180  4
## texp in (1 + sex + extrav + texp | class)     11 -2416.6 4855.3  0.060  4
##                                             Pr(>Chisq)    
## <none>                                                    
## sex in (1 + sex + extrav + texp | class)        0.8408    
## extrav in (1 + sex + extrav + texp | class)  3.312e-10 ***
## texp in (1 + sex + extrav + texp | class)       0.9996    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Através do teste fica evidente que o único slope significativo é o vindo de extrav, pois seu p valor < 0,05. Temos então a fórmula: popular ∼ 1 + sex + texp + extrav + (1 + extrav|class)
• A partir da fórmula descrita acima, criamos um Modelo Linear Misto, que recebe esse nome porque, dentre seus parâmetros, há tanto efeitos fixos quanto efeitos aleatórios. Nesse modelo, o efeito fixo é o sexo do aluno, a experiência do seu professor e seu grau de extroversão, mas se considera, ao mesmo tempo, variabilidade por classe por grau de extroversão.

Aplicando com lme4

model <- lmer(formula = popular ~ 1 + sex + extrav + texp + (1 + extrav| class),
               data    = popular2data)

summary(model)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: popular ~ 1 + sex + extrav + texp + (1 + extrav | class)
##    Data: popular2data
## 
## REML criterion at convergence: 4834.8
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.1768 -0.6475 -0.0235  0.6648  2.9684 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr 
##  class    (Intercept) 1.30299  1.1415        
##           extrav      0.03455  0.1859   -0.89
##  Residual             0.55209  0.7430        
## Number of obs: 2000, groups:  class, 100
## 
## Fixed effects:
##              Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept) 7.361e-01  1.966e-01 1.821e+02   3.745 0.000242 ***
## sex         1.252e+00  3.657e-02 1.913e+03  34.240  < 2e-16 ***
## extrav      4.526e-01  2.461e-02 9.750e+01  18.389  < 2e-16 ***
## texp        9.098e-02  8.685e-03 1.017e+02  10.475  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##        (Intr) sex    extrav
## sex    -0.031              
## extrav -0.717 -0.057       
## texp   -0.688 -0.039  0.086

• Caso nosso modelo obtive um overfit (funcionando muito bem para esta amostra em particular, mas não permite generalizações para a população de onde os dados foram obtidos), recebiamos o seguinte alerta: “## boundary (singular) fit: see ?isSingular”.
• Como não foi o caso seguimos com a análise desse modelo. Através do valor podemos observar que todos os efeitos fixos foram significativos, e anteriormente foi visto que o efeito aleatório também.

Analisando o modelo

• Como o summary não retorna o ajuste do nosso modelo podemos calculalo:

pred <- predict(model, type = "response")
resp <- popular2data$popular
cor(pred,resp)^2

## [1] 0.7330734

Comparação por modelos aninhados

• Caso queira testar se um determinado fator fixo é de fato significativo para o modelo em questão podemos fazer a comparação por modelos aninhados.
• Isso é feito por um teste de razão de verossimilhança. Nas palavras de Winter (2013):
  “Verossimilhança é a probabilidade de ver seu conjunto de dados dado o seu modelo. A lógica do teste de razão de verossimilhança é comparar a verossimilhança de dois modelos entre si. Primeiro, o modelo sem o fator de interesse (…), e depois o modelo com o fator em que se está interessado”
• Suponha que desejamos testar se a experiência do professor é significativo, devemos criar dois modelos, um com texto e outro sem! Na sequência, o teste de razão de verossimilhança é feito com a função anova(). Esse tipo de comparação é chamada de comparação de modelos aninhados pelo fato de o modelo mais simples estar contido (i.e., aninhado) no modelo mais completo.

## criando modelo completo e modelo aninhado

modelo.nulo  <- lmer(formula = popular ~ 1 + sex + extrav + (1+ extrav|class),
                     data  = popular2data, REML = FALSE)

modelo.texp <- lmer(formula = popular ~ 1 + sex + extrav + texp + (1+ extrav|class),
                     data  = popular2data, REML = FALSE)

## comparação de modelos
anova(modelo.nulo, modelo.texp)

## Data: popular2data
## Models:
## modelo.nulo: popular ~ 1 + sex + extrav + (1 + extrav | class)
## modelo.texp: popular ~ 1 + sex + extrav + texp + (1 + extrav | class)
##             Df    AIC    BIC  logLik deviance  Chisq Chi Df Pr(>Chisq)    
## modelo.nulo  7 4873.1 4912.3 -2429.6   4859.1                             
## modelo.texp  8 4828.8 4873.6 -2406.4   4812.8 46.323      1  1.003e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• As colunas AIC e BIC são estatísticas chamadas Akaike Information Criteria e Bayaesian Information Criteria. Elas servem como auxiliares na escolha do melhor modelo para os dados analisados. Não existe um valor de referência para estas estatísticas. Vamos escolher os modelos que possuam o menor valor de AIC ou BIC.
• Entretanto, esta decisão precisa ser tomada a partir de um teste de hipóteses realizado por meio de um Teste de Razão de Verossimilhanças, cujo valor está na coluna Pr(>Chisq). Como foi menor que 0.05 podemos confirmar que texto é significativo.

## $class

Análise de resíduo

• Homoteticidade: resíduos devem estar dispersos, sem padrões.
• Normalidade resíduos
• Normalidade efeitos aleatórios

Fazendo a previsão com o modelo

• A fórmula abaixo:

pred <- predict(model, type = "response"
                #newdata = ...
                )

Nem sempre é aplicável para banco de dados grandes, ou as vezes demanda de muito tempo computacional, nesse caso podemos fazer a predição manualmente.

• Quando desejamos ir além da análise do comportamento dos fatores, e usar o modelo para fazer previsões de novos dados podemos extrair os ranefs.

Ranef_classe <- 
  data.frame(
    class=rownames(ranef(model)$class), 
    Int_classe=ranef(model)$class[,2], 
    extrav_class=ranef(model)$class[,1]
  )

Ranef_classe %>% head(10)

##    class   Int_classe extrav_class
## 1      1 -0.009962121  -0.55757957
## 2      2  0.007645745  -0.69876452
## 3      3  0.145673570  -1.14517346
## 4      4 -0.063415991   0.51332720
## 5      5  0.234199649  -0.58842549
## 6      6  0.074538681  -0.39216643
## 7      7 -0.142620248  -0.09782894
## 8      8  0.165578304  -1.88137801
## 9      9  0.031936286   0.10554475
## 10    10 -0.177518771   0.66963848

• Armazenamos as estimativas do fator aleatório para cada classe, como é tratado como uma variável aleatória iremos considerar que cada classe possui um intercepto (Int_classe) e um grau de declividade (extrav_class) diferente.
• Vou criar um conjunto de 3 alunos, com características diferentes, e fazer a previsibilidade dos seus respectivos graus de popularidade:

novos_alunos = data.frame(
  row.names = c("João", "Maria", "Claudia"),
  "class"   = c('1', '4', '5'),
  "extrav"  = c(10, 2, 6),
  "sex" = c(0, 1 , 1),
  "texp" = c(10, 15, 8)
)

novos_alunos

##         class extrav sex texp
## João        1     10   0   10
## Maria       4      2   1   15
## Claudia     5      6   1    8

summary(model)$coefficients

##               Estimate  Std. Error         df   t value      Pr(>|t|)
## (Intercept) 0.73614952 0.196586862  182.09945  3.744653  2.421594e-04
## sex         1.25225444 0.036573241 1913.09435 34.239635 8.111296e-201
## extrav      0.45261994 0.024613832   97.53865 18.388845  1.819715e-33
## texp        0.09097566 0.008685065  101.65668 10.474955  7.516098e-18

• Vamos utilizar os coeficientes do modelo para os efeitos fixos, e para o efeito aleatório o ranef_class acima.

novos_alunos %>% 
  left_join(Ranef_classe, by = "class") %>% #juntando com os rafenfs de suas respectivas classes
  mutate(class = as.numeric(class)) %>% 
  mutate(
  popularidade_predita = (
    summary(model)$coefficients[1, 1] + # intercepto
    summary(model)$coefficients[2, 1]*sex +
    summary(model)$coefficients[3, 1]*extrav +
    summary(model)$coefficients[4, 1]*texp +
    Int_classe + # intercepto classes
    extrav_class*`class`
))

##   class extrav sex texp   Int_classe extrav_class popularidade_predita
## 1     1     10   0   10 -0.009962121   -0.5575796             5.604564
## 2     4      2   1   15 -0.063415991    0.5133272             6.248172
## 3     5      6   1    8  0.234199649   -0.5884255             2.724001