Artigo desenvolvido com a colaboração de André Calaça
O ponto principal do artigo a seguir é saber qual cálculo de tamanho de amostra utilizar, pois existem várias fórmulas, métodos e programas.
Como saber qual cálculo de amostra utilizar?
Para encontrar o tamanho de amostra de seu estudo, primeiramente você deve responder às seguintes perguntas:
- Qual o objetivo do meu estudo?
- Qual o tipo de estudo estou conduzindo?
- Qual método estatístico irei utilizar para atender meus objetivos?
- Qual a natureza da minha variável de interesse?
As respostas irão lhe conduzir para o melhor método de cálculo de tamanho de amostra para seu estudo. Embora seja complexo, não é impossível!
Assim, dado o objetivo da sua pesquisa, você irá conduzir um diferente tipo de estudo. Pensando em cálculo de tamanho de amostra é importante a seguinte divisão: Estudos Descritivos e Estudos Analíticos.
Estudos Descritivos
Os Estudos Descritivos têm como objetivo estimar um parâmetro, como a média ou uma proporção, para caracterizar uma variável dentro da população. Temos diversos estudos desse tipo, como por exemplo: pesquisa eleitoral; estimação da prevalência de determinada doença; uso médio de determinado produto diariamente e até encontrar a proporção de pessoas em cada faixa de renda de uma determinada cidade. Ou seja, a ideia é caracterizar uma população a partir de uma amostra.
Estudos Analíticos
Os Estudos Analíticos envolvem o uso de diferentes ferramentas estatísticas para testar as hipóteses de interesse. Sendo assim, seus objetivos dependem da classificação do estudo em observacional ou experimental.
Primordialmente, o objetivo do estudo observacional é verificar a associação entre variáveis, comparar grupos e encontrar padrões. Temos como exemplo desse estudo: verificar relação que existe entre qualidade de vida e nível educacional; comparar a performance de alunos entre escolas, verificar o impacto de indicadores sobre o NPS de uma empresa e segmentar os tipos de clientes de uma empresa.
No estudo experimental, você conduz um experimento planejado de forma a minimizar efeitos de confusão e viés, encontrando, dessa forma, uma relação de causa e efeito. Esse estudo não só é mais caro como também mais complexo. Alguns casos que utilizam o estudo experimental são: verificar o efeito de um medicamento sobre determinada doença; verificar quanto a temperatura impacta em uma determinada reação química; comparar o efeito de diferentes dietas sobre pessoas acima do peso e comparar o tempo de processamento computacional sobre diferentes cenários.
Especialmente em epidemiologia, existe um maior detalhamento desses tipos de estudos, como se pode ver na figura abaixo:
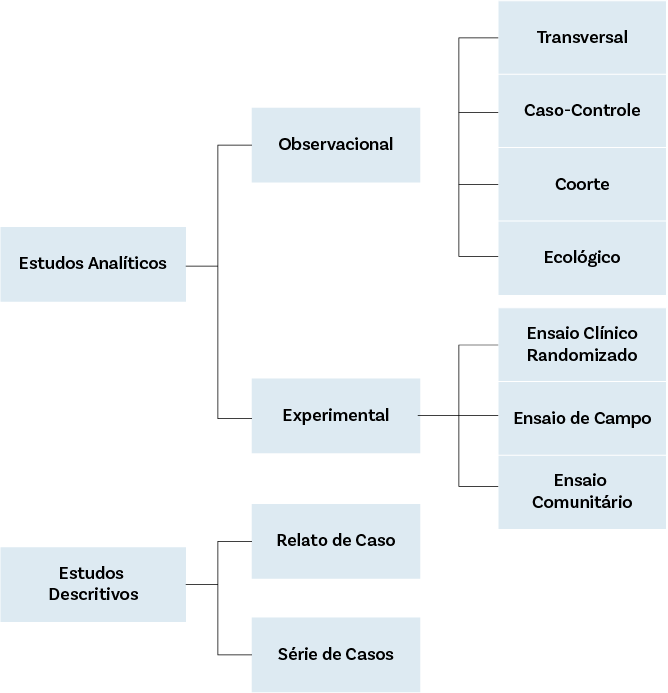
Estudos analíticos, descritivos, observacionais e experimental, são universais, ou seja, se aplicam para qualquer área do conhecimento. Para cálculo de tamanho de amostra, o que vai importar é colocar dentro de estudos analíticos e descritivos.
Divisão dos estudos
Os tipos de estudos descritivos se dividem se a análise for de um único indivíduo (Relato de Caso) ou de um pequeno grupo (Série de Casos).
Os estudos observacionais se dividem em Transversal, que pode ser um retrato da situação, uma Coorte, acompanhamento de indivíduos (geralmente expostos e não expostos, que pode ser de forma prospectiva ou retrospectiva), Caso-Controle (comparação de características de indivíduos que possui a doença com os que não a possuem), e os Ecológicos, em que a unidade amostral geralmente é um grupo de pessoas pertencentes a uma área geográfica.
Já os Experimentais, se dividem se as amostras são pacientes (Ensaio Clínico Randomizado), se são pessoas livres da doença (Ensaio de Campo) ou se a intervenção são feitas em comunidade (Ensaio de Comunidade).
Embora tenhamos apresentado diferentes tipos de estudos, é preciso separar somente em Descritivo ou Analítico para distinguir qual caminho tomar para definir o tipo de cálculo de tamanho de amostra para o seu estudo.
Na figura abaixo, pode-se visualizar os dois grandes grupos, e o que ainda é importante definir para se calcular o tamanho da amostra.
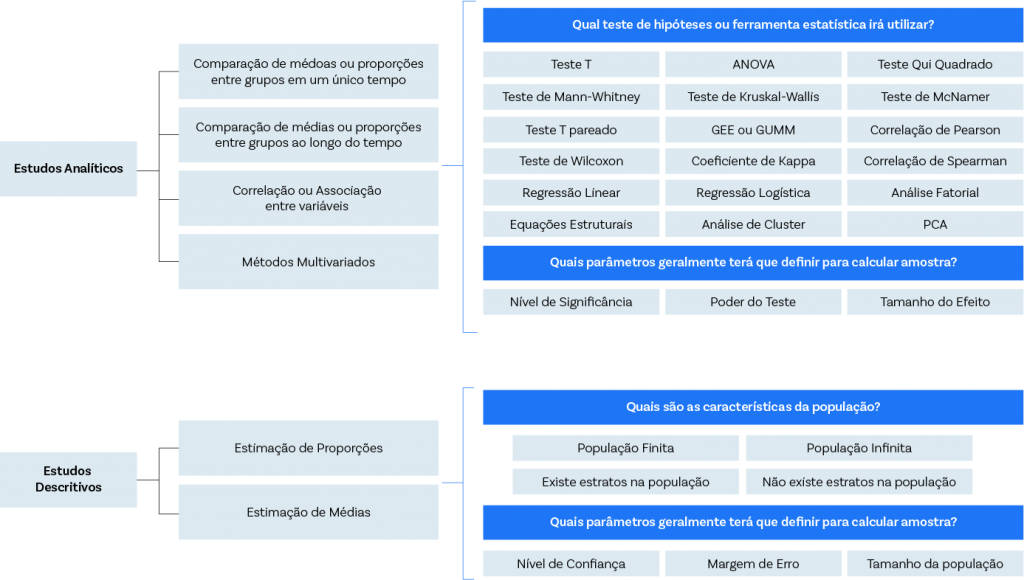
Estudo Analítico e seu cálculo
Quando estamos dentro de um estudo analítico, definimos qual caminho tomar; se vamos comparar média, proporções, relações entre as variáveis e se os métodos são multivariáveis. Em estudos descritivos, geralmente, estima-se proporções ou médias, entendendo qual tipo de variável é adequada.
O cálculo do tamanho da amostra depende do método que se utiliza.
Sendo assim, quando estamos dentro do universo de estudos analíticos, é necessário calcular o tamanho de uma amostra. Além do teste, é verificada sua significância, poder e tamanho do efeito.
Estudo descritivo e seu cálculo
Já em estudos descritivos, precisamos saber principalmente se a população é finita ou infinita. O tamanho da população é muito importante para calcular o tamanho da amostra e quais parâmetros são importantes. Assim, a definição do nível de confiança, margem de erro e tamanho da população são indispensáveis.
Tamanho de amostra para estudo descritivos
O desfecho dicotômico é a variável binária (o que mais é usado). Seguindo assim, desfecho numérico -onde a média é definida- desvio padrão da variável e a margem de erro.
*A correção para população finita é válida para estudos descritivos.
Quando optar por um cálculo do tamanho da amostra usando esse método, o resultado será grande o suficiente para associar ao poder adequado.
desfecho dicôtomico n=p(1-p)z² 1-a/2 sob d²
desfecho númerico n= s² z² 1-a/2 sob d²
correção para população finita n= N*n sob N+n
Tamanho de amostra para cálculo de estudos analíticos
Usar ferramentas estatísticas é o principal. Dessa forma, um pacote que ajuda bastante e tem diversas funções dentro dele é o PWR, capaz de calcular valores de amostra para os métodos apresentados na figura abaixo.
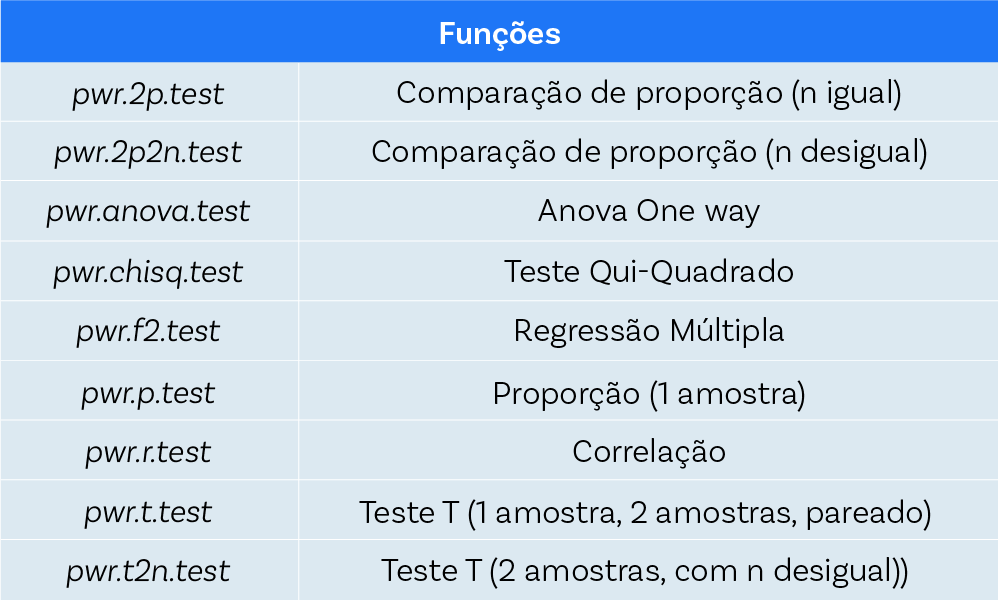
Teste T= comparação de médias entre dois grupos. De acordo com o Cohen, pode-se considerar 0,2, 0.5, 0.8 como tamanhos de efeito pequeno, médio e grande respectivamente. *Quando estamos trabalhando com teste t, é importante saber o tamanho do efeito, o poder do teste e o nível de significância. Lembre-se que para cada tipo de teste o efeito pode mudar;
0.2- pequeno 0.5- médio 0.8- grande
require (pwr)## loading required package: pwrpwr.t.test (d=0.5, sig.level = 0.05, power = 0.8 , type c('two.simple)) ## Tamanho de efeito ## ##
## Two-sample t test power calculation
##
## n= 63,76561
## d= 0,5
## sig.level= 0,05
## power= 0,8
## alternative= two.sided
##
## NOTE: n is in "each" grouppwr.t.test (d= 0,8 , sig.level = 0.05 , power = 0.8, type = c("paired")) ## Tamanho de efeito grande ##Um estudo anterior deve ser feito para calcular o tamanho de efeito (a diferença mínima que o teste irá detectar). O teste pareado sempre tem mais poder do que um teste para duas amostras, visto que dois grupos estão em pé de comparação.
##
## Two-sample t test power calculation
##
## n= 25,52458
## d= 0,8
## sig.level= 0,05
## power= 0,8
## alternative= two.sided
##
## NOTE: n is in "each" grouppwr.t.test (d= 0,8 , sig.level = 0.05 , power = 0.8, type = c("paired")) ## Tamanho de efeito grande ####
## paired t test power calculation
##
## n= 14,30276
## d= 0,8
## sig.level= 0,05
## power= 0,8
## alternative= two.sided
##
## NOTE: n is number of "pairs"ANOVA
O tamanho do efeito para comparação de médias entre mais de 2 grupos, considerando uma ANOVA, é dado por:
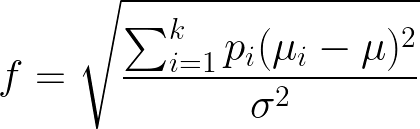
Nesse caso, pi= proporção do tamanho da amostra em cada grupo, e a2= desvio padrão dentre os grupos.
De acordo com Cohen, são considerados 0.1; 0.25; 0.4 como tamanhos de efeito pequeno, médio e grande respectivamente.
pwr.anova.test (k= 4 , sig.level = 0.05 , power = 0.8, f= 0.25) ## Tamanho de efeito médio (cohen 1988) ####
## Balanced one-way analysis of variance power calculation
##
## k=4
## n= 44,59927
## f= 0,25
## sig.level= 0,05
## power= 0,8
##
## NOTE: n is number in each grouppwr.anova.test (k= 4 , sig.level = 0.05 , power = 0.8, f= 0.4) ## Tamanho de efeito médio (cohen 1988) ####
## Balanced one-way analysis of variance power calculation
##
## k=4
## n= 18,04262
## f= 0,4
## sig.level= 0,05
## power= 0,8
##
## NOTE: n is number in each groupCorrelações
O tamanho de efeito é dado pela própria correlação. De acordo com Cohen 0.1; 0.3 e 0.5 são tamanhos de efeito pequeno, médio e grande respectivamente
pwr.r.test (r =0.3 , sig.leve = 0.05, power= 0.9)##
## approximate correlation power calculation (arctangh transformation)
##
## n= 111,8068
## r= 0,3
## sig.level= 0,05
## power= 0,9
## alternative = two. sidedPode parecer um pouco complexo no começo, mas tudo fica mais claro conforme o tempo passa e você se aprofunda no assunto. Ficou alguma dúvida? Deixe aqui embaixo nos comentários!