Artigo escrito com a colaboração de Joziani Mota Vieira
As filas estão presentes no nosso dia a dia e no geral acontecem porque a procura por um serviço é maior do que a capacidade do sistema de atender os clientes. Aumentar a capacidade de atendimento muitas vezes não é possível por limitações físicas ou econômicas. Por isso, a Teoria das Filas tenta, a partir de análises matemáticas detalhadas, encontrar um ponto de equilíbrio que satisfaça o cliente e seja viável para o provedor do serviço.
Modelos de filas
Os modelos de filas são definidos a partir da Notação de Kendall, que representa cada cadeia de filas pelos símbolos da seguinte forma: A/B/c/K/N/Z
- A: distribuição do tempo entre chegadas;
- B: disciplina de serviços;
- c: número de servidores;
- K: capacidade total de usuários no sistema;
- N: número de usuários potenciais em uma população fonte;
- Z: disciplina de atendimento.
Usualmente, quando não declarados a capacidade máxima do sistema (K), e o número de clientes a serem atendidos (N), estes serão considerados como ilimitados.
A disciplina de atendimento pode admitir duas politicas. First In First Out (primeiro que entra primeiro a sair), ou fila, é a estrutura de atendimento que bancos e hospitais utilizam, pois seguem a ordem de que os primeiros a chegar serão os primeiros a ser atendidos. Last In First Out (último que entra primeiro a sair) é a estrutura habitualmente chamada de pilha e amplamente utilizada na estacagem de produtos. Caso o modelo não declare qual a disciplina de atendimento, entende-se que será utilizada a disciplina FIFO.
Modelo M/M/2
O modelo M/M/2 da notação de Kendall é uma parametrização simples. Neste caso, a distribuição do tempo entre novas chegadas de clientes ao sistema é suposta exponencial (M). O tempo necessário para realizar cada serviço também segue uma distribuição exponencial (M). A capacidade máxima do sistema e a população fonte são supostamente infinitas. Nas aplicações desse modelo, denotamos por λλ e μμ a taxa média de chegada e de atendimento, respectivamente. Além disso, supomos que há dois servidores e que a disciplina da fila é FIFO.
Exemplo no R
Para exemplificarmos essa teoria vamos usar o R e simular as chegadas, atendimentos e saídas em um banco.
rm(list = ls())
if(!require(queuecomputer)){install.packages("queuecomputer");require(queuecomputer)}
if(!require(ggplot2)){install.packages("ggplot2");require(ggplot2)}
# Taxa de chegada
l = c(1/10, 1/3, 1/5, 1/8, 1/8, 1/5, 1/3)
# Taxa de Serviço
mu = 1/5
# Duração da simulação
duration = 60
time=0
# Chegadas antes do banco abrir
T1 = 0
while(time<duration){
T1 = c(T1,ceiling(rexp(1, rate = l[1])))
time <- sum(T1)
}
T1=T1[-length(T1)]
time <- sum(T1)
nEvents = length(T1) # número total de eventos ocorridos
antes=nEvents #número de pessoas que chegaram antes do banco abrir
#simulando as chegadas nas proximas 6 horas
for (i in 2:7) {
while(time<duration*i){
T1 = c(T1,(ceiling(rexp(1, rate = l[i]))))
time <- sum(T1)
}
T1=T1[-length(T1)]
}
T1=T1[-length(T1)]
T1## [1] 0 18 5 5 3 9 6 3 3 9 1 1 2 2 1 1 7 4 1 2 2 1 1
## [24] 1 3 1 5 1 3 3 3 1 2 2 2 1 3 4 2 3 3 31 2 4 12 8
## [47] 28 5 3 2 8 4 5 11 4 5 12 7 11 5 13 7 3 6 16 5 3 2 1
## [70] 2 2 6 1 1 1 1 16 7 4 3 4 5 1 2 9time <- sum(T1)
time## [1] 418nEvents = length(T1)
nEvents## [1] 85#simulando os atendimentos
atend = ceiling(rexp(1, rate = mu))
for (i in 2:nEvents) {
atend=c(atend,ceiling(rexp(1, rate = mu)))
}
atend## [1] 3 3 10 6 18 2 5 12 3 12 2 5 1 1 1 6 3 3 1 1 9 2 1
## [24] 5 9 8 8 5 13 9 5 3 5 3 13 2 7 1 2 4 4 4 7 2 5 1
## [47] 5 3 4 1 4 4 1 1 3 1 10 1 20 1 2 29 3 2 1 6 4 5 3
## [70] 3 1 4 8 1 1 1 2 10 3 1 6 2 9 18 7atend_antes=c(atend[1:antes])
atend_antes## [1] 3 3 10 6 18 2 5#Simulação de Chegadas
print("Simulação de Chegadas")## [1] "Simulação de Chegadas"cat("Chegada 1:" ,T1[1], "minutos", "\n")## Chegada 1: 0 minutosfor (i in 2:nEvents) {
a=i-1
cat("Chegada" , i,":" ,T1[i], "minutos","após chegada" ,a, "\n")
}## Chegada 2 : 18 minutos após chegada 1
## Chegada 3 : 5 minutos após chegada 2
## Chegada 4 : 5 minutos após chegada 3
## Chegada 5 : 3 minutos após chegada 4
## Chegada 6 : 9 minutos após chegada 5
## Chegada 7 : 6 minutos após chegada 6
## Chegada 8 : 3 minutos após chegada 7
## Chegada 9 : 3 minutos após chegada 8
## Chegada 10 : 9 minutos após chegada 9
## Chegada 11 : 1 minutos após chegada 10
## Chegada 12 : 1 minutos após chegada 11
## Chegada 13 : 2 minutos após chegada 12
## Chegada 14 : 2 minutos após chegada 13
## Chegada 15 : 1 minutos após chegada 14
## Chegada 16 : 1 minutos após chegada 15
## Chegada 17 : 7 minutos após chegada 16
## Chegada 18 : 4 minutos após chegada 17
## Chegada 19 : 1 minutos após chegada 18
## Chegada 20 : 2 minutos após chegada 19
## Chegada 21 : 2 minutos após chegada 20
## Chegada 22 : 1 minutos após chegada 21
## Chegada 23 : 1 minutos após chegada 22
## Chegada 24 : 1 minutos após chegada 23
## Chegada 25 : 3 minutos após chegada 24
## Chegada 26 : 1 minutos após chegada 25
## Chegada 27 : 5 minutos após chegada 26
## Chegada 28 : 1 minutos após chegada 27
## Chegada 29 : 3 minutos após chegada 28
## Chegada 30 : 3 minutos após chegada 29
## Chegada 31 : 3 minutos após chegada 30
## Chegada 32 : 1 minutos após chegada 31
## Chegada 33 : 2 minutos após chegada 32
## Chegada 34 : 2 minutos após chegada 33
## Chegada 35 : 2 minutos após chegada 34
## Chegada 36 : 1 minutos após chegada 35
## Chegada 37 : 3 minutos após chegada 36
## Chegada 38 : 4 minutos após chegada 37
## Chegada 39 : 2 minutos após chegada 38
## Chegada 40 : 3 minutos após chegada 39
## Chegada 41 : 3 minutos após chegada 40
## Chegada 42 : 31 minutos após chegada 41
## Chegada 43 : 2 minutos após chegada 42
## Chegada 44 : 4 minutos após chegada 43
## Chegada 45 : 12 minutos após chegada 44
## Chegada 46 : 8 minutos após chegada 45
## Chegada 47 : 28 minutos após chegada 46
## Chegada 48 : 5 minutos após chegada 47
## Chegada 49 : 3 minutos após chegada 48
## Chegada 50 : 2 minutos após chegada 49
## Chegada 51 : 8 minutos após chegada 50
## Chegada 52 : 4 minutos após chegada 51
## Chegada 53 : 5 minutos após chegada 52
## Chegada 54 : 11 minutos após chegada 53
## Chegada 55 : 4 minutos após chegada 54
## Chegada 56 : 5 minutos após chegada 55
## Chegada 57 : 12 minutos após chegada 56
## Chegada 58 : 7 minutos após chegada 57
## Chegada 59 : 11 minutos após chegada 58
## Chegada 60 : 5 minutos após chegada 59
## Chegada 61 : 13 minutos após chegada 60
## Chegada 62 : 7 minutos após chegada 61
## Chegada 63 : 3 minutos após chegada 62
## Chegada 64 : 6 minutos após chegada 63
## Chegada 65 : 16 minutos após chegada 64
## Chegada 66 : 5 minutos após chegada 65
## Chegada 67 : 3 minutos após chegada 66
## Chegada 68 : 2 minutos após chegada 67
## Chegada 69 : 1 minutos após chegada 68
## Chegada 70 : 2 minutos após chegada 69
## Chegada 71 : 2 minutos após chegada 70
## Chegada 72 : 6 minutos após chegada 71
## Chegada 73 : 1 minutos após chegada 72
## Chegada 74 : 1 minutos após chegada 73
## Chegada 75 : 1 minutos após chegada 74
## Chegada 76 : 1 minutos após chegada 75
## Chegada 77 : 16 minutos após chegada 76
## Chegada 78 : 7 minutos após chegada 77
## Chegada 79 : 4 minutos após chegada 78
## Chegada 80 : 3 minutos após chegada 79
## Chegada 81 : 4 minutos após chegada 80
## Chegada 82 : 5 minutos após chegada 81
## Chegada 83 : 1 minutos após chegada 82
## Chegada 84 : 2 minutos após chegada 83
## Chegada 85 : 9 minutos após chegada 84#Simulação de Atendimentos
print("Simulação de Atendimentos")## [1] "Simulação de Atendimentos"cat("Atendimento 1: " ,atend[1], "minutos", "\n")## Atendimento 1: 3 minutosfor (i in 2:nEvents) cat("Atendimento" ,i,":" ,atend[i], "minutos","\n")## Atendimento 2 : 3 minutos
## Atendimento 3 : 10 minutos
## Atendimento 4 : 6 minutos
## Atendimento 5 : 18 minutos
## Atendimento 6 : 2 minutos
## Atendimento 7 : 5 minutos
## Atendimento 8 : 12 minutos
## Atendimento 9 : 3 minutos
## Atendimento 10 : 12 minutos
## Atendimento 11 : 2 minutos
## Atendimento 12 : 5 minutos
## Atendimento 13 : 1 minutos
## Atendimento 14 : 1 minutos
## Atendimento 15 : 1 minutos
## Atendimento 16 : 6 minutos
## Atendimento 17 : 3 minutos
## Atendimento 18 : 3 minutos
## Atendimento 19 : 1 minutos
## Atendimento 20 : 1 minutos
## Atendimento 21 : 9 minutos
## Atendimento 22 : 2 minutos
## Atendimento 23 : 1 minutos
## Atendimento 24 : 5 minutos
## Atendimento 25 : 9 minutos
## Atendimento 26 : 8 minutos
## Atendimento 27 : 8 minutos
## Atendimento 28 : 5 minutos
## Atendimento 29 : 13 minutos
## Atendimento 30 : 9 minutos
## Atendimento 31 : 5 minutos
## Atendimento 32 : 3 minutos
## Atendimento 33 : 5 minutos
## Atendimento 34 : 3 minutos
## Atendimento 35 : 13 minutos
## Atendimento 36 : 2 minutos
## Atendimento 37 : 7 minutos
## Atendimento 38 : 1 minutos
## Atendimento 39 : 2 minutos
## Atendimento 40 : 4 minutos
## Atendimento 41 : 4 minutos
## Atendimento 42 : 4 minutos
## Atendimento 43 : 7 minutos
## Atendimento 44 : 2 minutos
## Atendimento 45 : 5 minutos
## Atendimento 46 : 1 minutos
## Atendimento 47 : 5 minutos
## Atendimento 48 : 3 minutos
## Atendimento 49 : 4 minutos
## Atendimento 50 : 1 minutos
## Atendimento 51 : 4 minutos
## Atendimento 52 : 4 minutos
## Atendimento 53 : 1 minutos
## Atendimento 54 : 1 minutos
## Atendimento 55 : 3 minutos
## Atendimento 56 : 1 minutos
## Atendimento 57 : 10 minutos
## Atendimento 58 : 1 minutos
## Atendimento 59 : 20 minutos
## Atendimento 60 : 1 minutos
## Atendimento 61 : 2 minutos
## Atendimento 62 : 29 minutos
## Atendimento 63 : 3 minutos
## Atendimento 64 : 2 minutos
## Atendimento 65 : 1 minutos
## Atendimento 66 : 6 minutos
## Atendimento 67 : 4 minutos
## Atendimento 68 : 5 minutos
## Atendimento 69 : 3 minutos
## Atendimento 70 : 3 minutos
## Atendimento 71 : 1 minutos
## Atendimento 72 : 4 minutos
## Atendimento 73 : 8 minutos
## Atendimento 74 : 1 minutos
## Atendimento 75 : 1 minutos
## Atendimento 76 : 1 minutos
## Atendimento 77 : 2 minutos
## Atendimento 78 : 10 minutos
## Atendimento 79 : 3 minutos
## Atendimento 80 : 1 minutos
## Atendimento 81 : 6 minutos
## Atendimento 82 : 2 minutos
## Atendimento 83 : 9 minutos
## Atendimento 84 : 18 minutos
## Atendimento 85 : 7 minutosfilas <- queue_step(arrivals=T1, service=atend, servers=2)
filas## # A tibble: 85 x 6
## arrivals service departures waiting system_time server
## <dbl> <dbl> <dbl> <dbl> <dbl> <int>
## 1 0 3 3 0 3 1
## 2 18 3 210 189 192 1
## 3 5 10 136 121 131 2
## 4 5 6 136 125 131 1
## 5 3 18 78 57 75 2
## 6 9 2 172 161 163 1
## 7 6 5 151 140 145 1
## 8 3 12 90 75 87 1
## 9 3 3 81 75 78 2
## 10 9 12 184 163 175 1
## # ... with 75 more rowssummary(filas)## Total customers:
## 85
## Missed customers:
## 0
## Mean waiting time:
## 91.8
## Mean response time:
## 96.8
## Utilization factor:
## 0.995327102803738
## Mean queue length:
## 37.2
## Mean number of customers in system:
## 38.4Gráficos da espera em filas
## parcelas de densidade dos horários de chegada e partida
plot(filas, which = 1)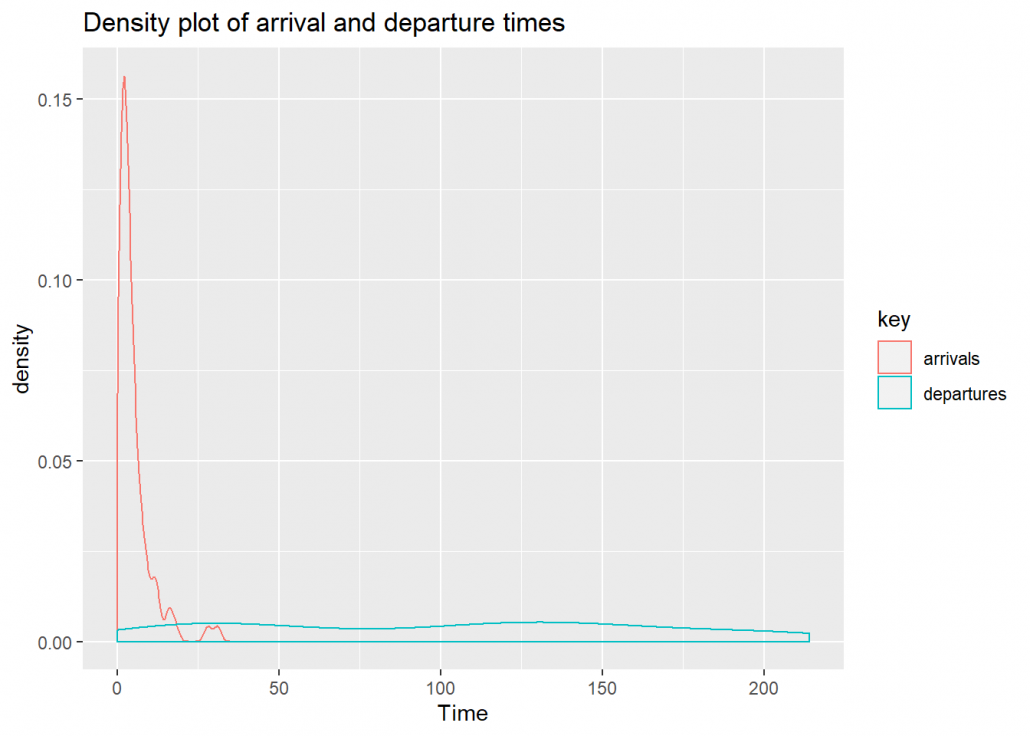
## histogramas dos horários de chegada e partida
plot(filas, which = 2)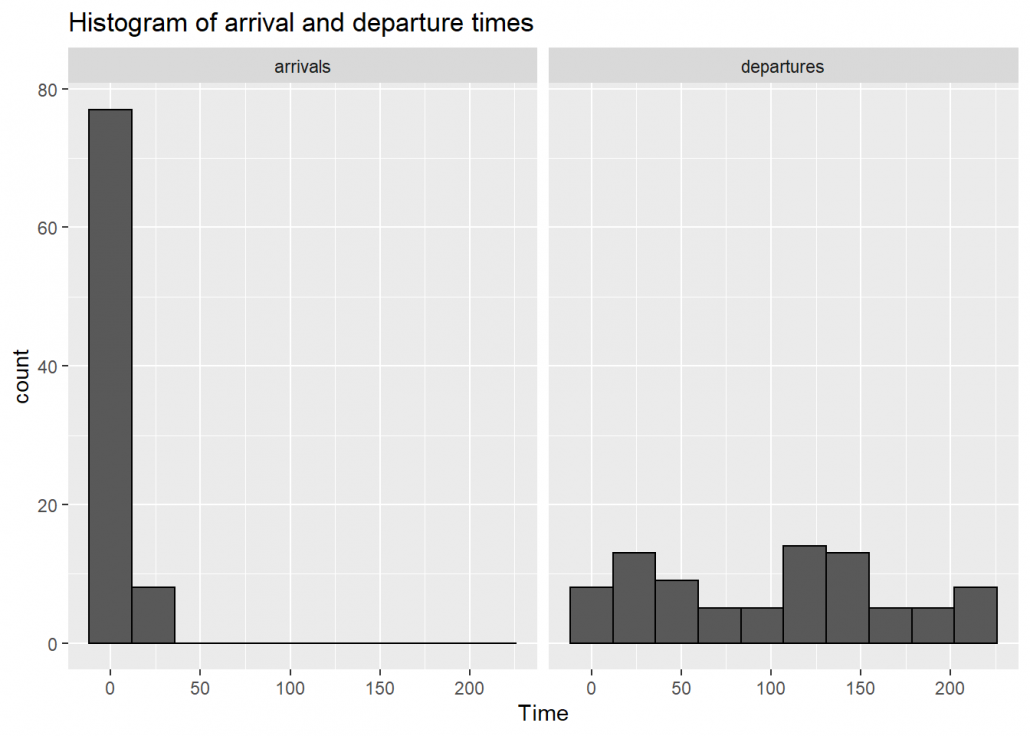
## gráficos de densidade de tempos de espera e sistema
plot(filas, which = 3)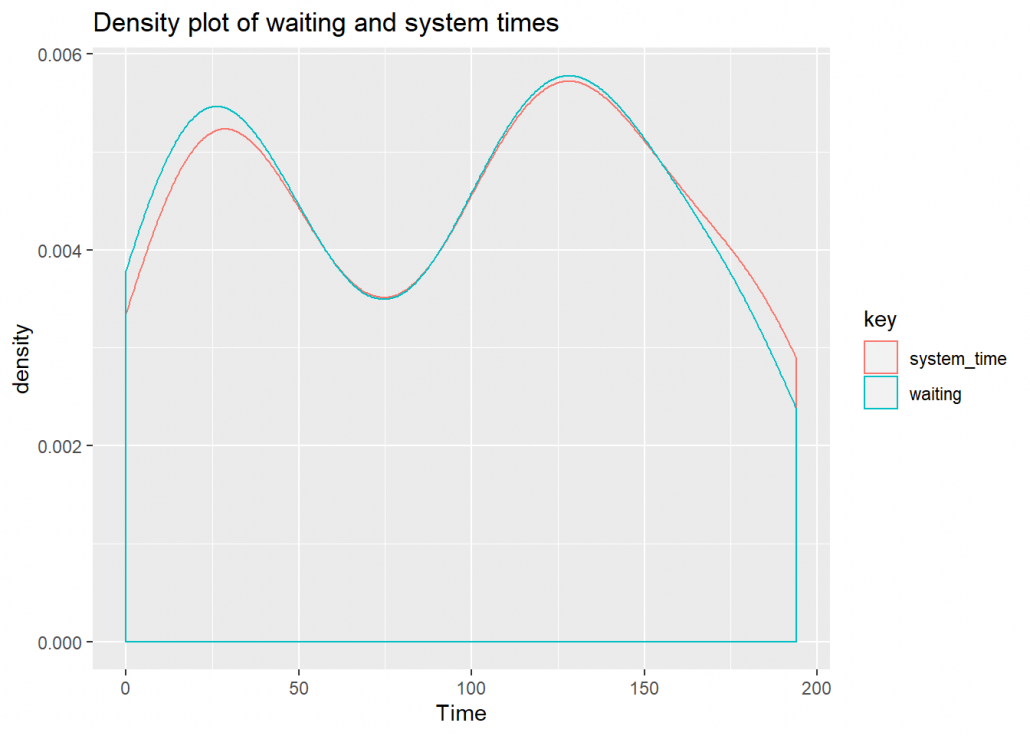
## função step do comprimento da fila
plot(filas, which = 4)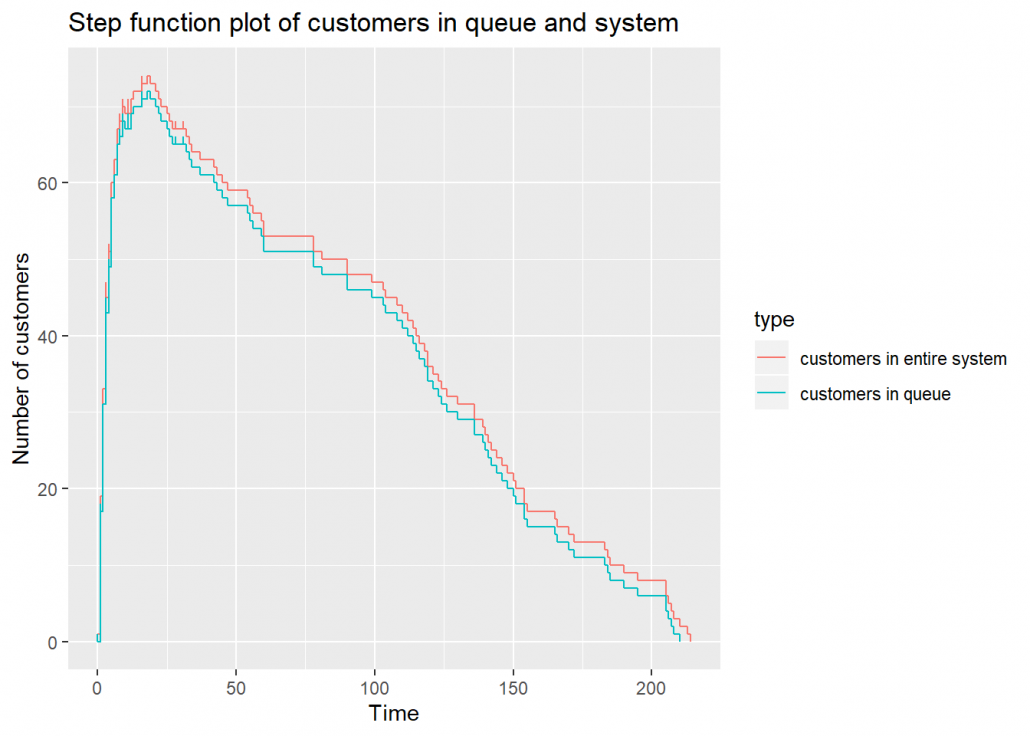
## gráfico de intervalo de linhas do status do cliente e do servidor
plot(filas, which = 5)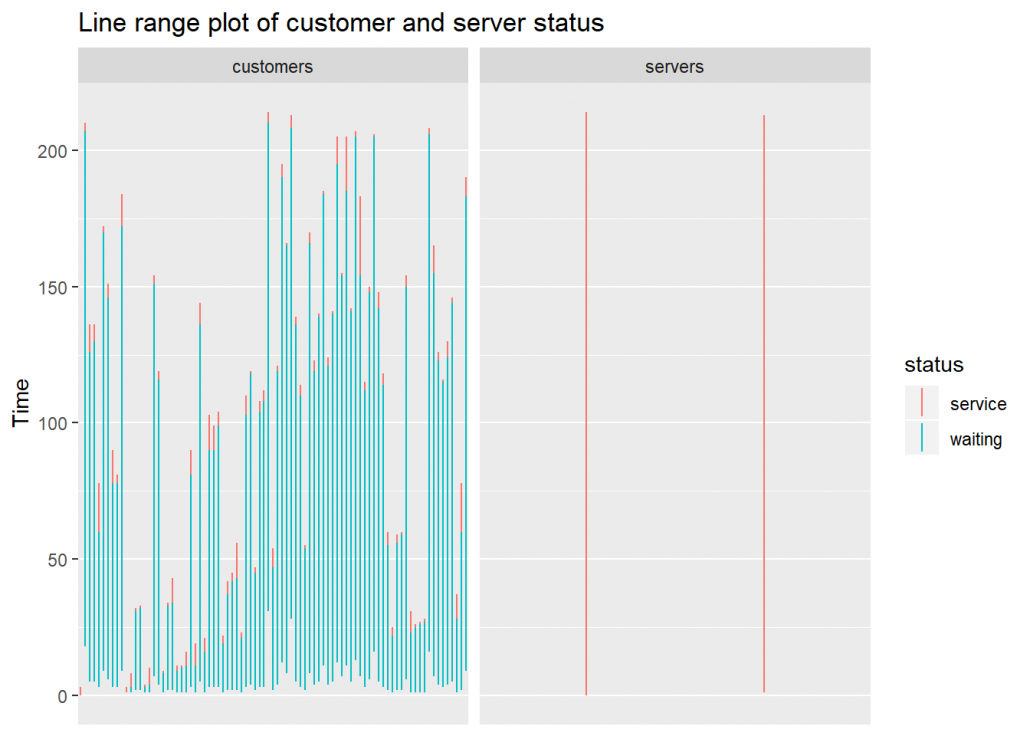
## gráfico de distribuição empírica dos horários de chegada e partida
plot(filas, which = 6)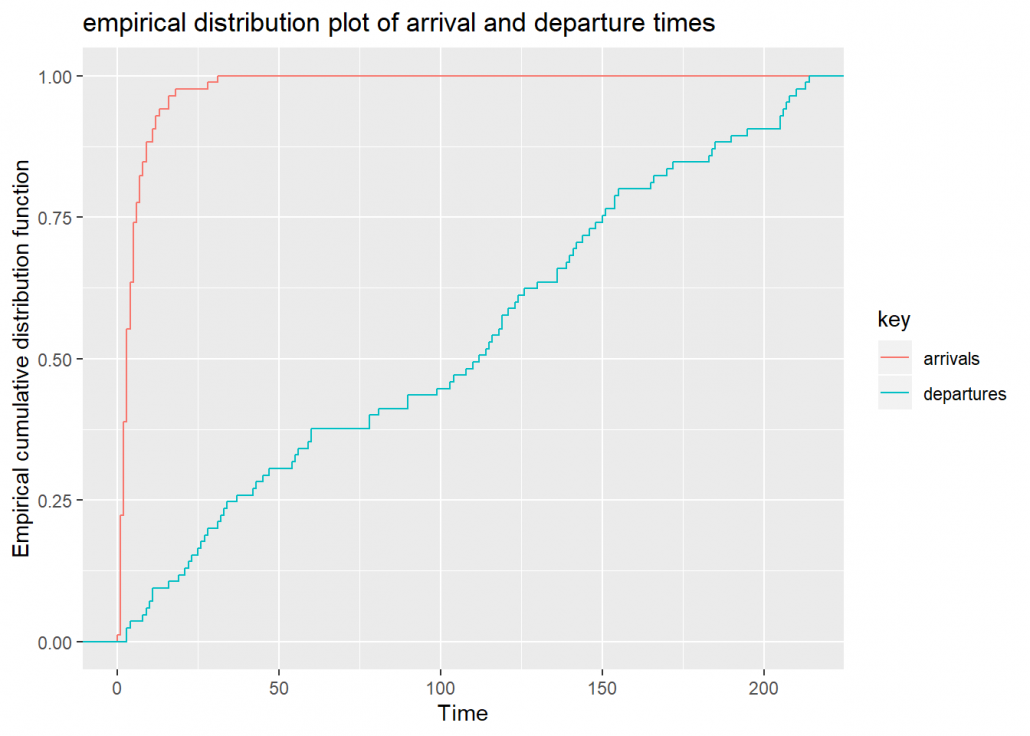
Você já conseguiu entender um pouco mais sobre a teoria das filas? Restou alguma dúvida? Deixe seus comentários aqui embaixo que iremos responder.