Você sobreviveria no Titanic? Um exemplo de Regressão Logística

A tragédia do Titanic, em 1912, é um dos desastres marítimos mais conhecidos da história. Eternizado no cinema em 1997, o navio construído em Belfast (Irlanda) naufragou quatro dias após o início da sua viagem inaugural, que tinha como destino a cidade de Nova Iorque.

Quando construído, o navio prometia ser o mais luxuoso e seguro de sua época. Entretanto, estudos posteriores indicaram falhas no sistema de segurança e evacuação. A estimativa é de 1514 mortes entre os 2224 passageiros, ou seja, aproximadamente 68% da tripulação. E hoje, por meio da regressão logística podemos prever a chance que qualquer pessoa teria de sobreviver à tragédia.

Caso você estivesse no navio, qual seria a sua chance de sobrevivência?

A Regressão Logística faz parte de uma família de modelos chamada Modelos Lineares Generalizados (GLM) e é adequada quando a variável de interesse (resposta) é binária, isto é, “sim” ou “não”. Através da Regressão Logística é possível avaliar os fatores que influenciam a ocorrência de determinado evento.

Neste caso, a variável resposta é a morte ou a sobrevivência do passageiro. Disponível na internet, há um banco de dados referente a 891 indivíduos que estavam na tripulação do navio. O banco está disponível no Kaggle e é necessário o cadastro no site para o download gratuito da base. No banco de dados em questão, estão disponíveis algumas informações sobre os tripulantes, mas neste exemplo consideraremos suas respectivas idade, sexo, classe (1ª à 3ª) e desfecho (morte ou sobrevivência). Dessa forma, é possível calcular a probabilidade de sobrevivência do indivíduo a partir destas características.

Na base de dados faltam registros sobre a idade de 177 indivíduos e, como o objetivo é uma análise didática, os mesmos foram excluídos das análises. Dessa forma, as análises seguintes são referentes a 714 passageiros do navio (cerca de 32% do total de tripulantes). Vale ressaltar que existem técnicas mais sofisticadas para o tratamento de dados perdidos, que podem ser discutidas posteriormente em nossos artigos.

Função de Ligação da Regressão Logística e a Razão de Chances

Como uma característica do GLM, a Regressão Logística utiliza a função de ligação “logit”, o que possibilita a interpretação dos resultados em função da Razão de Chances (Odds Ratio).

A função de ligação conecta os fatores de influência à variável resposta. Por exemplo, na Regressão Linear Simples, que não possui nenhuma função de ligação, a variável de interesse (resposta) pode assumir qualquer valor nos números reais e, dessa forma, a função de ligação “logit” limita os valores previstos pelo modelo ao intervalo 0 e 1, como uma característica da resposta. A Razão de Chances pode ser definida como a razão de um evento ocorrer em um grupo A em função de um grupo B.

Como mostrado nos momentos finais do filme estrelado por Leonardo DiCaprio e Kate Winslet, mulheres e crianças eram prioridade na evacuação do navio. Dessa forma, é esperado que a chance de sobrevivência dos indivíduos do sexo feminino (grupo A) seja superior a chance de sobrevivência do sexo masculino (grupo B). Neste caso, por exemplo, a Razão de Chances da variável ‘sexo’, em relação a variável resposta, seria a razão entre a chance de sobrevivência de indivíduos do sexo feminino e masculino.

Características da tripulação

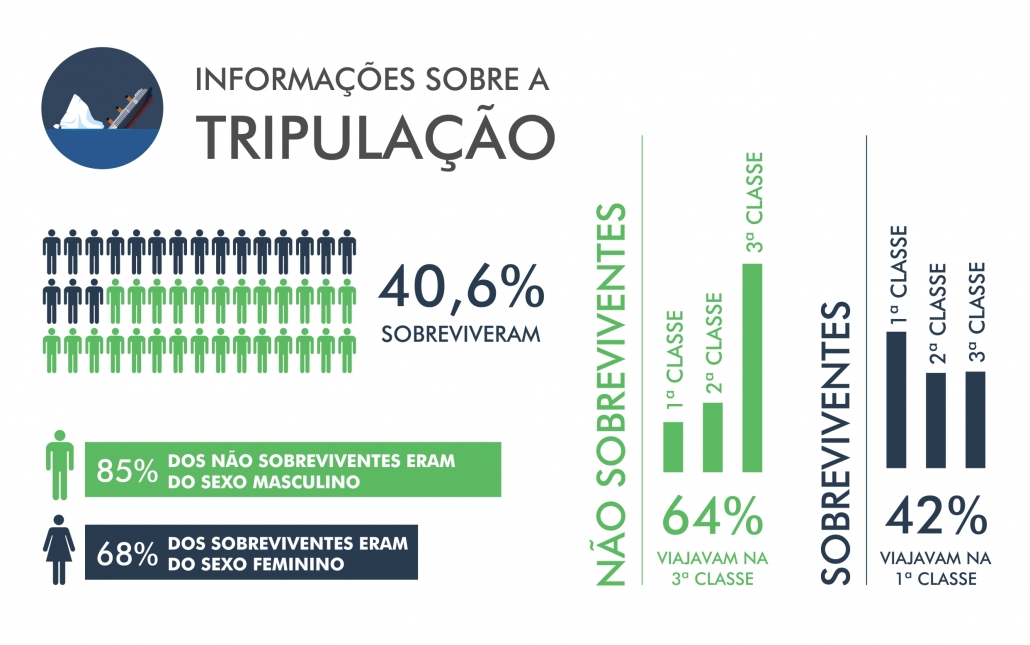
Na amostra, 424 indivíduos (59,38%) não sobreviveram e 290 (40,62%) sobreviveram. Cerca de 68% dos sobreviventes eram do sexo feminino e 85% dos não sobreviventes eram do sexo masculino. Em relação a classe, 42% dos sobreviventes eram da 1ª classe e 64% dos não sobreviventes eram da 3ª classe.

A idade média dos indivíduos que não sobreviveram foi de 30,62 anos, sendo a idade mínima de 1 ano e a máxima de 74 anos. A Idade média dos indivíduos que sobreviveram foi de 28,24 anos, sendo a idade mínima menor que 1 ano e a máxima de 80 anos.

Ajuste do modelo logístico

O ajuste do modelo é mostrado abaixo e é possível observar que todas as variáveis foram significativas ao nível de 5% de significância (valor-p < 0,050). Logo, a chance de sobrevivência para indivíduos do sexo feminino foi 12,46 [8,3; 18,71] vezes maior que a chance de sobrevivência para os indivíduos do sexo masculino.

Em relação a chance de sobrevivência dos indivíduos da 3ª a classe, a chance de sobrevivência para os indivíduos da 2ª classe foi 3,36 [2,21; 5,75] vezes maior e para os indivíduos da 1ª classe a chance de sobrevivência foi 13,21 [7,61; 22,93] vezes maior. Sobre a idade, a cada ano acrescido na idade do indivíduo a chance de sobrevivência foi 0,96 [0,95; 0,98] vezes menor.

Variáveis	β	E.P.(β)	O.R.	I.C. – 95%	Valor P
Sexo = Masculino	–	–	1,00	–	–
Sexo = Feminino	2,52	0,21	12,46	[8,3 ; 18,71]	0,000
Classe = 3ª	–	–	1,00	–	–
Classe = 2ª	1,27	0,24	3,56	[2,21 ; 5,75]	0,000
Classe = 1ª	2,58	0,28	13,21	[7,61 ; 22,93]	0,000
Idade	-0,04	0,01	0,96	[0,95 ; 0,98]	0,000

Equação do Modelo de Regressão Logística

Sendo g(X) a função de ligação, a equação do modelo é dada por:

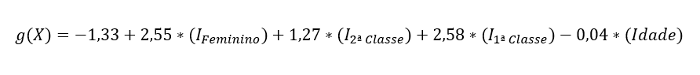
“I_Feminino“ recebe 1 se o indivíduo é do sexo feminino e 0 se é do sexo masculino, “I_{2ª Classe}“ recebe 1 se o indivíduo navegava na 2ª classe e 0 caso contrário e “I_{1ª Classe}“ recebe 1 se o indivíduo navegava na 1ª classe e 0 caso contrário.

Para calcular a probabilidade de sobrevivência de um indivíduo, E(Y) , é necessário aplicar uma função inversa a função de ligação, sendo representada por:

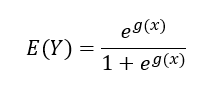
Dessa forma, uma mulher de 42 anos que estava na 1ª classe tem probabilidade de sobrevivência de 0,90, enquanto que uma mulher de mesma idade na 3ª classe tem probabilidade de sobrevivência de 0,41. Um homem de 30 anos de idade da 1ª classe tem probabilidade de sobrevivência de 0,42, enquanto que um homem de mesma idade na 2ª classe tem probabilidade de sobrevivência de 0,16.

Rose DeWitt Bukater, interpretada por Kate Winslet, era uma garota de 17 anos que estava na primeira classe. Jack Dawson, interpretado por Leonardo DiCaprio, tinha 20 anos e estava na terceira classe. Segundo o modelo logístico, a probabilidade de sobrevivência de Rose é de aproximadamente 0,96, enquanto que a probabilidade de sobrevivência de Jack é de aproximadamente 0,11.

Qual seria a sua probabilidade de sobrevivência?

Elaboramos uma calculadora para que você saiba qual seria a sua probabilidade de sobrevivência caso estivesse viajando no Titanic.

Informe a sua idade: -- Selecione -- Menos de um ano 1 Ano 2 Anos 3 Anos 4 Anos 5 Anos 6 Anos 7 Anos 8 Anos 9 Anos 10 Anos 11 Anos 12 Anos 13 Anos 14 Anos 15 Anos 16 Anos 17 Anos 18 Anos 19 Anos 20 Anos 21 Anos 22 Anos 23 Anos 24 Anos 25 Anos 26 Anos 27 Anos 28 Anos 29 Anos 30 Anos 31 Anos 32 Anos 33 Anos 34 Anos 35 Anos 36 Anos 37 Anos 38 Anos 39 Anos 40 Anos 41 Anos 42 Anos 43 Anos 44 Anos 45 Anos 46 Anos 47 Anos 48 Anos 49 Anos 50 Anos 51 Anos 52 Anos 53 Anos 54 Anos 55 Anos 56 Anos 57 Anos 58 Anos 59 Anos 60 Anos 61 Anos 62 Anos 63 Anos 64 Anos 65 Anos 66 Anos 67 Anos 68 Anos 69 Anos 70 Anos 71 Anos 72 Anos 73 Anos 74 Anos 75 Anos 76 Anos 77 Anos 78 Anos 79 Anos 80 Anos 81 Anos 82 Anos 83 Anos 84 Anos 85 Anos 86 Anos 87 Anos 88 Anos 89 Anos 90 Anos 91 Anos 92 Anos 93 Anos 94 Anos 95 Anos 96 Anos 97 Anos 98 Anos 99 Anos
Informe o seu sexo: -- Selecione -- Masculino Feminino
Em qual classe você estaria navegando? -- Selecione -- Primeira Classe Segunda Classe Terceira Classe
Calcular

A aplicação ao evento de morte no Titanic é apenas um exemplo ilustrativo. Caso queira saber mais sobre o modelo de regressão logística, entre em contato! E não deixe de se inscrever em nosso blog para conferir nossos artigos!

Artigo desenvolvido com a colaboração de Leonardo Gonçalves.