Artigo escrito com a colaboração de Luis Henrique Velasquez.
De forma bem simples, o Machine Learning se baseia na construção e no uso de algoritmos que “aprendem” a partir dos dados.
Os problemas de Machine Learning são divididos em três subáreas principais: classificação, regressão e clustering. Já falamos aqui no blog sobre a Classificação e no artigo de hoje vamos continuar explicando Regressão e Clustering.
Machine Learning é um assunto vasto e que se aproxima muito da estatística já que os modelos dependem muito das técnicas estatísticas bem desenvolvidas.
Regressão
A Regressão é um dos métodos de previsão mais utilizados no meio estatístico. Tem como principal objetivo verificar como certas variáveis de interesse influenciam uma variável resposta Y e criar um modelo matemático capaz de predizer valores de Y com base em novos valores de variáveis preditoras X.
Regressão Linear Simples
O modelo de regressão simples pode ser escrito da seguinte forma:
yi = β0 + β1xi + εi
Sendo que os erros são identicamente distribuídos, seguindo uma distribuição Normal com média 0 e variância σ². (εi ~ N(0,σ²)).
O foco desse seminário não será entrar em muitos detalhes acerca da teoria estatística por trás da regressão, mas sim mostrar pontos uteis para um melhor uso no R.
Os principais métodos utilizados para avaliar o desempenho dos modelos de regressão são:
- RMSE: ou Raiz do Erro Quadrático Médio, é comumente usada para expressar a acurácia dos resultados numéricos do modelo. Como já explicado na seção das medidas de desempenho, quando maior seu valor, pior o desempenho do modelo.
- R²: expressa a porcentagem de variância explicada pelas variáveis independentes apresentadas no modelo. Quando maior, melhor o desempenho dele. Porém, é importante verificar a significância e a quantidade dessas variáveis antes de verificar o R² do modelo, dado que um aumento do número de variáveis acaba por acarretar um aumento dessa medida.
O código abaixo utiliza o banco de dados “kang.nose” para construirmos uma regressão linear simples, criando um modelo que prevê a largura do nariz de cangurus com base em seu comprimento. Realizaram-se predições do modelo através da função predict() e cálculos para as medidas de desempenho RMSE e R².
kang.nose %>% summary() nose_width nose_length
Min. :189,0 Min. :493,0
1st Qu.:220,0 1st Qu.:616,0
Median :237,0 Median :677,0
Mean :244,2 Mean :687,4
3rd Qu.:272,0 3rd Qu.:755,0
Max. :308,0 Max. :864,0 ### Aplicando um regressão linear simples - Witdh explicando por Length
mod.nose <- lm(nose_width ~ nose_length, data= kang.nose)
mod.nose %>% summary()
Call:
lm(formula = nose_width ~ nose_length, data = kang.nose)
Residuals:
Min 1Q Median 3Q Max
-29,656 -7,479 2,132 8,229 27,344
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 46,4508 16,2998 2,85 0,00669 **
nose_length 0,2876 0,0235 12,24 1,34e-15 ***
---
Signif. codes: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1
Residual standard error: 14,44 on 43 degrees of freedom
Multiple R-squared: 0,7769, Adjusted R-squared: 0,7717
F-statistic: 149,7 on 1 and 43 DF, p-value: 1,342e-15mod.nose$coefficients # retorna os coeficientes(Intercept) nose_length
46,4508136 0,2876124 new_length <- data.frame(nose_length = c(500, 600, 700)) # Novos dados
predict(mod.nose, new_length, interval = "confidence") # Previsão com base nos novos + IC 95% fit lwr upr
1 190,2570 180,3698 200,1442
2 219,0182 213,0172 225,0193
3 247,7795 243,3970 252,1619RMSE <- function(error) { sqrt(mean(error^2)) } # Função criada para o cálculo do RMSE
RMSE(mod.nose$residuals) # RMSE[1] 14,11701summary(mod.nose)$r.squared # R2[1] 0,7768914Regressão Linear Multivariada
A regressão linear multivariada é semelhante à simples, porém com mais de uma variável preditora. Para esse tipo de regressão, no lugar do R² utiliza-se o R² ajustado, já que ele consegue penalizar o acréscimo de variáveis ao modelo, fazendo com que não seja diretamente inflacionada nesse contexto.
No código abaixo, trabalharemos com o banco “shop.data”, que apresenta as vendas de uma loja com base em diversas características dos seus clientes. Assim como foi realizado com o caso da regressão linear simples, realizaremos previsões, calcularemos medidas de desempenho (como o R² ajustado) e verificaremos as suposições dos erros do modelo de regressão multivariada.
shop.data %>% summary() sales sq_ft inv ads
Min. : 0,5 Min. :0,500 Min. :102,0 Min. : 2,50
1st Qu.: 98,5 1st Qu.:1,400 1st Qu.:204,0 1st Qu.: 4,80
Median :341,0 Median :3,500 Median :382,0 Median : 8,10
Mean :286,6 Mean :3,326 Mean :387,5 Mean : 8,10
3rd Qu.:450,5 3rd Qu.:4,750 3rd Qu.:551,0 3rd Qu.:10,95
Max. :570,0 Max. :8,600 Max. :788,0 Max. :17,40
size_dist comp
Min. : 1,600 Min. : 0,000
1st Qu.: 4,500 1st Qu.: 4,000
Median :11,300 Median : 8,000
Mean : 9,693 Mean : 7,741
3rd Qu.:14,050 3rd Qu.:12,000
Max. :16,300 Max. :15,000 ### Aplicando uma regressão linear multivariada - Sales como variável resposta
mod.shop <- lm(sales ~ . , data = shop.data) # "~." mostra que usaremos todas as demais variáveis
mod.shop %>% summary()
Call:
lm(formula = sales ~ ., data = shop.data)
Residuals:
Min 1Q Median 3Q Max
-26,338 -9,699 -4,496 4,040 41,139
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -18,85941 30,15023 -0,626 0,538372
sq_ft 16,20157 3,54444 4,571 0,000166 ***
inv 0,17464 0,05761 3,032 0,006347 **
ads 11,52627 2,53210 4,552 0,000174 ***
size_dist 13,58031 1,77046 7,671 1,61e-07 ***
comp -5,31097 1,70543 -3,114 0,005249 **
---
Signif. codes: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1
Residual standard error: 17,65 on 21 degrees of freedom
Multiple R-squared: 0,9932, Adjusted R-squared: 0,9916
F-statistic: 611,6 on 5 and 21 DF, p-value: < 2,2e-16mod.shop$coefficients # retorna os coeficientes(Intercept) sq_ft inv ads size_dist comp
-18,8594073 16,2015726 0,1746352 11,5262679 13,5803127 -5,3109718 summary(mod.nose)$r.squared # R2 (aumenta com o acréscimo de variáveis)[1] 0,7768914summary(mod.nose)$adj.r.squared # R2 Ajustado[1] 0,7717028RMSE(mod.shop$residuals) # RMSE[1] 15,56517#### Verificando suposições dos resíduos
# Residuos independentemente distribuídos em torno de 0
plot(mod.shop$fitted.values, mod.shop$residuals)
abline(h=0, col="red", lty= 3) 
# Normalidade dos resíduos
if(!require(car)){ install.packages("car"); require(car) }
qqPlot(mod.shop$residuals)
[1] 6 17mod.shop$residuals %>% shapiro.test() # Rejeita a hipóte nula de normalidade
Shapiro-Wilk normality test
data: .
W = 0,91859, p-value = 0,03651K-Nearest Neighbors (KNN)
É importante observar que, assim como no método de Classificação, é possível utilizar o k-Nearest Neighbors (KNN) como uma forma de regressão não-paramétrica.
No código abaixo, usaremos um training e um test set já construídos para o banco de dados “world”, apresentando o cgdp (similar ao PIB) de diversos países e a sua porcentagem de população urbana. Utilizaremos a função knn.reg() (pacote “FNN”) para fazer previsões de “cgdp” (variável resposta) no test set após seu treinamento no training set. Utilizaram-se 20% do total de observações alocadas no training set para a definição do número k de vizinhos.
# Separando os preditores e a variável resposta dos sets
world.test.x <- world.test[,-1] %>% as.data.frame()
world.train.x <- world.train[,-1] %>% as.data.frame()
world.train.y <- world.train[,1] %>% as.data.frame()
world.test.y <- world.test[,1] %>% as.data.frame()
# KNN = knn("Training set","test set", "classificação real do training", "K vizinhos consiederados")
if(!require(FNN)){ install.packages("FNN"); require(FNN) }
knn.world = FNN::knn.reg(train = world.train.x, test = world.test.x, y = world.train.y, k = 28) # k=20% total obs training
knn.worldPrediction:
[1] 2510,690 2966,211 3153,116 4604,018 6490,574 2510,690 6490,574
[8] 18704,486 2553,522 32266,901 23111,132 3753,158 6532,045 16700,703
[15] 26601,322 32266,901 29289,700 16277,721 28704,561 28704,561 11953,832
[22] 24495,555 6490,574 2553,522 32266,901 18704,486 28704,561 29005,821
[29] 32266,901 32266,901 17764,754 5941,413 3047,800 3120,619 26673,573
[36] 24495,555 32266,901 32266,901 15285,950 3135,717 3038,616 23083,414
[43] 12493,242 11982,323 28704,561 5813,593 28704,561 28617,902 6939,055
[50] 7045,579 32266,901 5961,592 4123,500 12260,437 18704,486 32266,901
[57] 2975,100 32266,901 2915,870 2553,522 2868,928Clustering
O Clustering é uma subárea do Machine Learning de aprendizado não-supervisionado, visto que suas técnicas não necessitam de rótulos de classes (como no caso da classificação e regressão) para realizar suas previsões. Um Cluster é um objeto que contém diversas observações que são semelhantes entre si dentro desse cluster específico e diferentes de outras observações que foram alocadas em outros clusters. Dessa forma, o Clustering nada mais é que agrupar os dados em clusters baseado em suas características/variáveis. Como já comentado anteriormente, não existe propriamente uma clusterização certa ou errada dos dados, sendo que o tipo de clusterização utilizada resulta em diferentes tipos de clusters, e a escolha dessas técnicas devem ser previamente analisadas pelo pesquisador.
O objetivo do uso do Clustering é uma melhor visualização dos seus dados, estudando padrões de comportamento e detectando outliers. Para realizarmos o Clustering, usamos medidas de similaridade dos dados (como a distância Euclidiana para os dados numéricos ou variáveis dummys para variáveis categóricas) e técnicas como k-means e Clustering Hierárquico, que serão explicadas mais a frente.
Para que seja possível alcançar o melhor desempenho no processo de clusterização, necessitamos que os clusters apresentem a maior similaridade possível entre si em seu interior e que apresentem a maior diferença possível entre si ao serem comparados uns com os outros. Essa similaridade e dissimilaridade podem ser medidas a partir da “soma de quadrados dentro do Cluster” (WSS) e pela “soma de quadrados entre os clusters” (BSS), que medem a compacidade e a separação dos clusters, respectivamente. Suas fórmulas são apresentadas na imagem abaixo:

K-means
A técnica K-means tem como objetivo separar os dados em k clusters diferentes, com base em k-centroides. Seu algoritmo funciona da seguinte forma:
1. Gera-se aleatoriamente k-centroides.
2. Atribuí-se os dados aos centroides mais próximos, criando-se clusters.
3. Move-se os centroides para a localização média de cada um dos k clusters criados no passo 2, colocando-os no centro real desses clusters criados.
4. Repetem-se os passos 2 e 3 n vezes (a escolha do usuário) ou até que não se ocorra mais mudanças significativas nas posições dos k centroides.
A melhor escolha do “k” (número de clusters) é baseado na escolha que apresente a minimização do WSS. Porém, quanto maior o k, menor tende a ser o WSS. Para resolver esse problema, escolhemos o k quando a sua diminuição começa a ser muito pequena mesmo com o aumento no número de clusters. O critério usualmente utilizado para essa diminuição é escolher K quando a razão entre o WSS e o TSS (que consiste na soma do WSS com o BSS) for menor que 0,2. O Scree Plot apresenta o gráfico dessa razão em relação a k, e a principal forma gráfica de selecionar-se o k ideal: o k ideal será quando se forma o “cotovelo” da curva apresentada, pois é o momento em que a razão começa a decrescer de forma mais suave.
A imagem abaixo mostra um exemplo desse gráfico: a partir do ponto k = 3, existe uma diminuição bem menos expressiva da razão WSS/TSS, sendo assim a melhor escolha para o número de clusters nesse caso.

O código abaixo utiliza o banco de dados seeds, porém sem sua classificação anteriormente apresentada, e utiliza a função kmeans() (pacote “stats”) para construirmos 3 clusters diferentes. É importante salientar que, quando não indicado na função, o R seleciona aleatoriamente o centroide dos dados, o que pode alterar o cálculo dos clusters. Além disso, construiremos um algoritmo para a construção de um Scree Plot.
# Semente aleatória
set.seed(100)
# K-means construido para 3 clusters, repetindo 20 vezes (nstart), com centroide aleatoriamente selecionado ("centers" não definido)
seeds_km <- kmeans(seeds,3,nstart=20)
seeds_kmK-means clustering with 3 clusters of sizes 72, 77, 61
Cluster means:
area perimeter compactness length width asymmetry groove_length
1 14,64847 14,46042 0,8791667 5,563778 3,277903 2,613892 5,192319
2 11,96442 13,27481 0,8522000 5,229286 2,872922 4,759740 5,088519
3 18,72180 16,29738 0,8850869 6,208934 3,722672 3,603590 6,066098
Clustering vector:
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1
[38] 3 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 1 1 1 1 1 2 3 3 3 3
[75] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 3 3
[112] 3 3 3 3 3 3 3 3 3 3 3 1 3 1 3 3 3 3 3 3 3 1 1 1 1 3 1 1 1 2 2 2 2 2 2 2 2
[149] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2
[186] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2
Within cluster sum of squares by cluster:
[1] 218,6106 195,7453 184,1086
(between_SS / total_SS = 78,1 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" seeds_km$betweenss # BSS[1] 2137,896seeds_km$tot.withinss # WSS[1] 598,4645# Comparando a clusterização realizada com a classificação real das sementes
table(seeds_km$cluster,seeds_type$seeds_type)
1 2 3
1 60 10 2
2 9 0 68
3 1 60 0# Plotando o comprimento das sementes em função da sua largura e colorindo de acordo com os clusters criados
plot(seeds$width,seeds$length,col=seeds_km$cluster)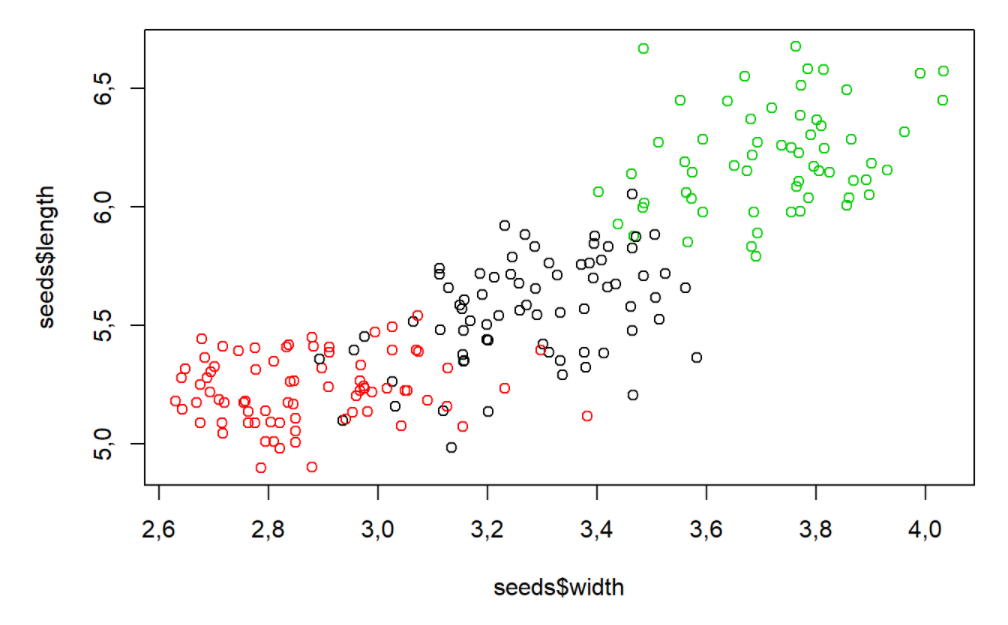
# Criando o Scree Plot para as sementes
Razão.seed <- rep(0,7) # Número total de clusters a serem testados no Scree Plot
for (k in 1:7) {
seeds_km <- kmeans(seeds,nstart=20,k) # Aplicando K-means
Razão.seed[k] <- seeds_km$tot.withinss/seeds_km$totss # Salvando a Razão WSS/TSS para cada k utilizado
}
plot(Razão.seed,type="b",xlab="k", main="Scree Plot para o banco Seeds") # K = 3 ou 4
abline(h=0.2, col="red", lty= 3)
Uma alternativa para se medir o desempenho da clusterização similar ao uso do BSS e WSS é o Dunn Index: essa estatística apresenta a razão entre a distância mínima entre os clusters e o diâmetro máximo dos clusters. Assim, um valor alto do Dunn Index mostra que os clusters em questão estão bem separados entre si e bem compactos. Porém, essa estatística tem um custo computacional alto (quando maior o número de clusters, maior o custo) e deve ser utilizada no pior caso.
O código abaixo utiliza o banco de dados run_record, apresentando o recorde de diversos tipos de maratonas. Usaremos a função dunn() (pacote “clValid”) para o cálculo do Dunn Index e a função scale() para o escalonamento das variáveis (iremos padronizar os dados, pois a escala entre os recordes se diferenciava substancialmente).
summary(run_record) # as escalas dos records se diferenciam muito! Country X100m X200m X400m X800m
Argentina: 1 Min. : 9,78 Min. :19,32 Min. :43,18 Min. :101,4
Australia: 1 1st Qu.:10,10 1st Qu.:20,17 1st Qu.:44,91 1st Qu.:103,8
Austria : 1 Median :10,20 Median :20,43 Median :45,58 Median :105,6
Belgium : 1 Mean :10,22 Mean :20,54 Mean :45,83 Mean :106,1
Bermuda : 1 3rd Qu.:10,32 3rd Qu.:20,84 3rd Qu.:46,32 3rd Qu.:108,0
Brazil : 1 Max. :10,97 Max. :22,46 Max. :51,40 Max. :116,4
(Other) :48
X1500m X5000m X10000m marathon
Min. :206,4 Min. : 759,6 Min. :1588 Min. : 7473
1st Qu.:213,0 1st Qu.: 788,9 1st Qu.:1653 1st Qu.: 7701
Median :216,6 Median : 805,2 Median :1675 Median : 7819
Mean :219,2 Mean : 817,1 Mean :1712 Mean : 8009
3rd Qu.:224,2 3rd Qu.: 834,5 3rd Qu.:1739 3rd Qu.: 8050
Max. :254,4 Max. :1002,0 Max. :2123 Max. :10276
# Semente aleatoria
set.seed(16)
# K-means para valores numéricos do run_record: 5 clusters, repetir 20 vezes
run_km <- kmeans(run_record[,2:9],nstart=20,5)
# Calculando o Dunn's index
if(!require(clValid)){ install.packages("clValid"); require(clValid) }
dunn_km <- dunn(clusters=run_km$cluster,Data=run_record[,2:9])
dunn_km[1] 0,05651773# Escalonizando os dados
run_record_sc <- as.data.frame(scale(run_record[2:9]))
# K-means: Run record escolonado
run_km_sc <- kmeans(run_record_sc,nstart = 20,5)
# Comparando os clusters do run record escalonado e não-escalonado
table(run_km$cluster,run_km_sc$cluster)
1 2 3 4 5
1 7 0 0 1 10
2 1 0 0 13 10
3 0 0 6 0 0
4 0 2 0 0 0
5 2 0 2 0 0# Calculando o Dunn index para o run record escalonizado
dunn_km_sc<-dunn(cluster=run_km_sc$cluster,Data=run_record_sc)
dunn_km_sc # O dunn escalonado é bem superior ao não escalonado[1] 0,1453556Clustering Hierárquico
Além da técnica do K-means, outra técnica importante no Clustering é o Clustering Hierárquico. Diferentemente da técnica K-means, o Clustering Hierárquico apresenta a ordem de junção dos objetos de cada cluster, assim como quais clusters se fundiram para a formação de um novo cluster, seguindo um comportamento hierárquico dos clusters. A hierarquia de formação dos clusters dependerá dos tipos de distâncias utilizadas para medir a similaridade entre os objetos. É importante observar que essa técnica consiste na formação de cluster através de passos, e cada cluster é formado separadamente seguindo-se uma hierarquia.
O algoritmo utilizado no Clustering Hierárquico funciona da seguinte forma:
- Antes de tudo, calcula-se a distância entre os objetos/observações.
1. Coloca-se cada objeto em seu próprio cluster.
2. Mescla-se o par de objetos mais próximos entre si. Demais objetos continuarão iguais.
3. Recalcula-se a distância entre o novo cluster formado e os demais objetos restantes.
4. Repetem-se os passos 2 e 3 até um critério de parada (geralmente, até a formação de um único cluster final).
Existem três métodos utilizados para determinar a ligação entre os objetos e formação dos clusters, sendo que cada um deles afeta diretamente na formação dos clusters:
- Simple-Linkage: a distância entre dois clusters é definida como a distância mínima encontrada entre os objetos de um dos clusters para os demais objetos do outro cluster.
- Complete-Linkage: a distância entre dois clusters é definida como a distância máxima encontrada entre os objetos de um dos clusters para os demais objetos do outro cluster.
- Average-Linkage: a distância entre dois clusters é definida como a distância média encontrada entre os objetos dos dois clusters.
Após a escolha do método de linkagem, construímos um gráfico chamado Dendrograma. Esse gráfico consegue nos mostrar a ordem das mesclas entre os objetos (barras horizontais), assim como a distância entre os clusters antes deles serem mesclados (altura do dendrograma). Pode-se “cortar” o dendrograma de acordo com o número de clusters desejado pelo pesquisador. A imagem abaixo nos dá a ideia de como esse gráfico é apresentado:

O código abaixo apresente a aplicação da técnica de Clustering Hierárquico no banco de dados “seeds”, que apresenta diversas características de 3 tipos de sementes, assim como sua classificação. Iremos utilizar esse banco de dados retirando a coluna referente a espécie das sementes para realizarmos previsões para suas classificações e depois as compararemos com suas classificações originais. Utilizaremos a função hclust() (pacote “stats”) para realizar o clustering hierárquico e a função cutree() (pacote “dendextend”) para o corte do dendrograma no número de clusters desejado (k = 3, referente ao número de espécies originalmente classificadas).
summary(seeds) # Analisando o banco de dados - verificando as escalas das variaveis area perimeter compactness length
Min. :10,59 Min. :12,41 Min. :0,8081 Min. :4,899
1st Qu.:12,27 1st Qu.:13,45 1st Qu.:0,8569 1st Qu.:5,262
Median :14,36 Median :14,32 Median :0,8734 Median :5,524
Mean :14,85 Mean :14,56 Mean :0,8710 Mean :5,629
3rd Qu.:17,30 3rd Qu.:15,71 3rd Qu.:0,8878 3rd Qu.:5,980
Max. :21,18 Max. :17,25 Max. :0,9183 Max. :6,675
width asymmetry groove_length
Min. :2,630 Min. :0,000077 Min. :4,519
1st Qu.:2,944 1st Qu.:2,561500 1st Qu.:5,045
Median :3,237 Median :3,599000 Median :5,223
Mean :3,259 Mean :3,688187 Mean :5,408
3rd Qu.:3,562 3rd Qu.:4,768750 3rd Qu.:5,877
Max. :4,033 Max. :8,456000 Max. :6,550 #### Como as variáveis estavam em escalas diferentes, escalonamos ela a partir da normalização
seeds_sc <- seeds %>% scale %>% as.data.frame()
summary(seeds_sc) # Todas escolonadas com média 0 e dp 1 area perimeter compactness length
Min. :-1,4632 Min. :-1,6458 Min. :-2,6619 Min. :-1,6466
1st Qu.:-0,8858 1st Qu.:-0,8494 1st Qu.:-0,5967 1st Qu.:-0,8267
Median :-0,1693 Median :-0,1832 Median : 0,1037 Median :-0,2371
Mean : 0,0000 Mean : 0,0000 Mean : 0,0000 Mean : 0,0000
3rd Qu.: 0,8446 3rd Qu.: 0,8850 3rd Qu.: 0,7100 3rd Qu.: 0,7927
Max. : 2,1763 Max. : 2,0603 Max. : 2,0018 Max. : 2,3619
width asymmetry groove_length
Min. :-1,6642 Min. :-2,41116 Min. :-1,8090
1st Qu.:-0,8329 1st Qu.:-0,73659 1st Qu.:-0,7387
Median :-0,0572 Median :-0,05831 Median :-0,3766
Mean : 0,0000 Mean : 0,00000 Mean : 0,0000
3rd Qu.: 0,8026 3rd Qu.: 0,70644 3rd Qu.: 0,9541
Max. : 2,0502 Max. : 3,11704 Max. : 2,3234 ### Calculando a distância entre os objetos (distância Euclidiana)
dist_mat <- dist(seeds_sc, method = 'euclidean')
#### Criando o dendrograma e testando cada um dos três métodos de ligação
if(!require(stats)){ install.packages("stats"); require(stats) }
hclust_single <- hclust(dist_mat, method = 'single') # Usa a Distancia mínima entre objetos
plot(hclust_single)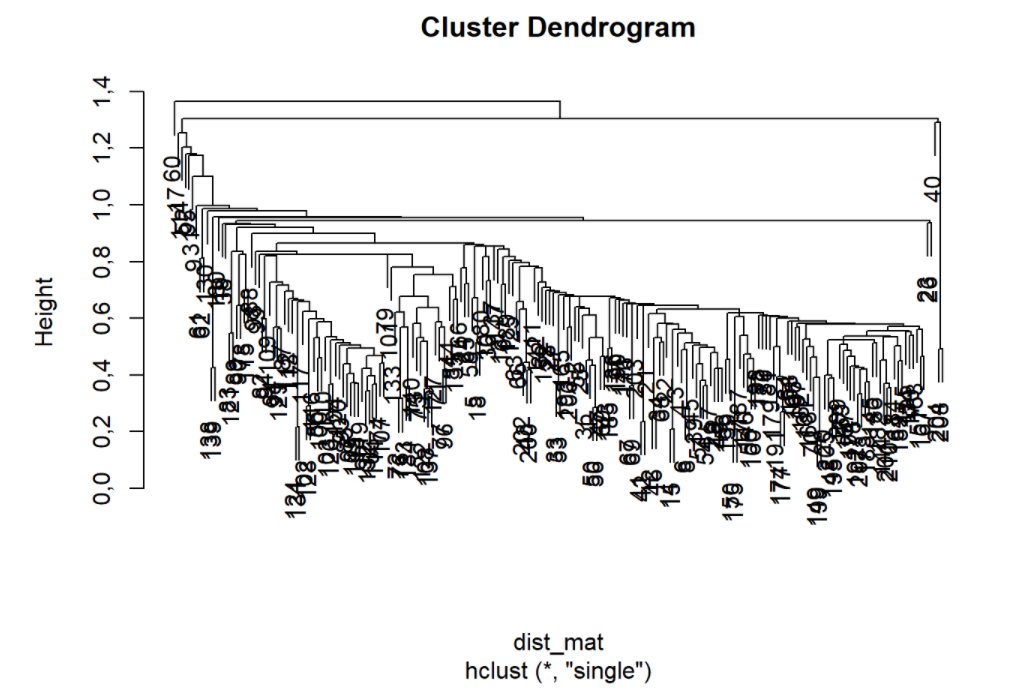
hclust_complete <- hclust(dist_mat, method = 'complete') # Usa a Distancia máxima entre objetos
plot(hclust_complete)
hclust_avg <- hclust(dist_mat, method = 'average') # Usa a Distancia média entre objetos
plot(hclust_avg)
### Dado que ja sabemos que os dados originais continham 3 tipos de sementes, vamos cortar o gráfico com k=3
if(!require(dendextend)){ install.packages("dendextend"); require(dendextend) }
cut_avg <- cutree(hclust_avg, k = 3) # Cortando o dendrograma que utilizou o médio "average"
### Colorindo os três clusters formados no dendograma via método "average"
avg_col_dend <- hclust_avg %>% as.dendrogram() %>% color_branches(h = 3) # Função que colore os clusters
plot(avg_col_dend)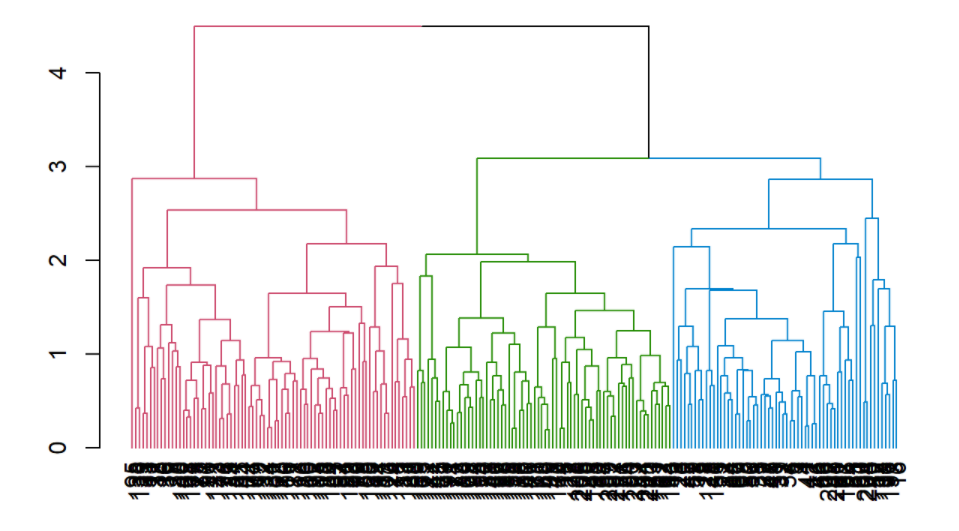
### Comparando com os clusters com seus rotulos originais
seeds_sc <- seeds_sc %>% mutate(cluster = cut_avg)
conf.seeds <- table(seeds_sc$cluster,seeds_type$seeds_type) # Cluster originais nas colunas
conf.seeds
1 2 3
1 52 2 8
2 10 68 0
3 8 0 62accuracy <- function(x){sum(diag(x)/(sum(rowSums(x)))) * 100} # Função para calcular a acurácia da previsão
accuracy(conf.seeds) # 86,67 % de acurácia [1] 86,66667