Modelos de Machine Learning utilizando o pacote Caret

Artigo escrito com a colaboração de Laura Kubitschek

O pacote caret, abreviação para “Classification And Regression Training”, possui uma série de funções para facilitar o processo e a construção de modelos preditivos. Nele existem ferramentas para divisão dos dados, pré-processamento, seleção de variáveis, ajuste de modelos utilizando reamostragem, estimativa da importância de variáveis e muitas outras funcionalidades.

Neste artigo, o objetivo é apresentar como alguns modelos de Machine Learning podem ser ajustados utilizando esse pacote de maneira simples, direta e bem intuitiva.

Sintaxe do Caret

Uma vez que o intuito do artigo é apresentar como ajustar modelos de Machine Learning usando o pacote, a diante vamos abordar a sintaxe do caret voltada para esse objetivo. No entanto, caso queira aprender mais sobre todas suas ferramentas sugiro essa bibliografia.

Construção de Modelos

A função train do pacote pode ser usada para:

• ajustar modelos e avaliar, usando reamostragem, os efeitos dos parâmetros de ajustes no desempenho do modelo;
• escolher o modelo ideal entre os parâmetros testados;
• estimar o desempenho do modelo a partir de um conjunto de treinamento.

A lógica de funcionamento do pacote é bem simples. No primeiro momento, deve-se escolher um modelo específico. Com o caret é possível ajustar 238 modelos diferentes (rode o código paste(names(getModelInfo())) para ver a lista de todos disponíveis). Cada modelo possui suas especificidades, sendo assim, utilizando o código modelLookup(nome do modelo), você tem acesso a mais informações, como , por exemplo, se ele pode ser usado para problemas de classificação e/ou regressão e os parâmetros do ajuste que podem ser otimizados.

É importante frizar que, ao rodar um modelo, o caret caham algum pacote secundário com as especificações de ajuste do modelo.

head(paste(names(getModelInfo())), n=15)

##  [1] "ada"         "AdaBag"      "AdaBoost.M1" "adaboost"    "amdai"      
##  [6] "ANFIS"       "avNNet"      "awnb"        "awtan"       "bag"        
## [11] "bagEarth"    "bagEarthGCV" "bagFDA"      "bagFDAGCV"   "bam"

modelLookup("rf")

##   model parameter                         label forReg forClass probModel
## 1    rf      mtry #Randomly Selected Predictors   TRUE     TRUE      TRUE

Uma vez que você escolheu qual modelo deseja ajustar, o próximo passo é escolher os valores dos parâmetros que deseja que o algoritmo avalie.

Em seguida, deve-se especificar o tipo de reamostragem que deve ser usado. A função train abrange os métodos de validação cruzada k-fold (uma vez ou com repetições), validação cruzada leave-one-out e bootstrap (estimação simples ou regra 632).

Após a reamostragem, o modelo ajustado retorna diversas medidas de desempenho para orientar a escolha do usuário em relação aos parâmetros de ajuste. Como padrão, a função seleciona os parâmetros associados ao melhor valor da medida de desempenho principal, sendo possível alterar essa medida de avaliação ou especificar diferentes algorítmos para a escolha dos melhores parâmetros.

Por fim, é ajustado um modelo final em todo banco treino utilizando os parâmetros “ótimos” escolhidos.

Exemplo Introdutório

A fim de introduzir a construção de modelos utilizando o pacote caret será mostrado a seguir um exemplo simples de um ajuste de random forest usando o banco de dados Sonar, disponível no pacote mlbench.

Carregando pacote e banco

A base Sonar faz parte de um estudo para classificação de sinais de sonar, com o objetivo de diferenciar o reconhecimento de rochas (“R”) e minas (“M”) a partir dos valores de 60 variáveis numéricas.

library(mlbench)
data(Sonar)
glimpse(Sonar[, 50:61])

## Rows: 208
## Columns: 12
## $ V50   <dbl> 0.0324, 0.0061, 0.0106, 0.0294, 0.0046, 0.0081, 0.0159, 0.017...
## $ V51   <dbl> 0.0232, 0.0125, 0.0033, 0.0241, 0.0156, 0.0104, 0.0195, 0.005...
## $ V52   <dbl> 0.0027, 0.0084, 0.0232, 0.0121, 0.0031, 0.0045, 0.0201, 0.008...
## $ V53   <dbl> 0.0065, 0.0089, 0.0166, 0.0036, 0.0054, 0.0014, 0.0248, 0.012...
## $ V54   <dbl> 0.0159, 0.0048, 0.0095, 0.0150, 0.0105, 0.0038, 0.0131, 0.004...
## $ V55   <dbl> 0.0072, 0.0094, 0.0180, 0.0085, 0.0110, 0.0013, 0.0070, 0.012...
## $ V56   <dbl> 0.0167, 0.0191, 0.0244, 0.0073, 0.0015, 0.0089, 0.0138, 0.009...
## $ V57   <dbl> 0.0180, 0.0140, 0.0316, 0.0050, 0.0072, 0.0057, 0.0092, 0.008...
## $ V58   <dbl> 0.0084, 0.0049, 0.0164, 0.0044, 0.0048, 0.0027, 0.0143, 0.004...
## $ V59   <dbl> 0.0090, 0.0052, 0.0095, 0.0040, 0.0107, 0.0051, 0.0036, 0.004...
## $ V60   <dbl> 0.0032, 0.0044, 0.0078, 0.0117, 0.0094, 0.0062, 0.0103, 0.005...
## $ Class <fct> R, R, R, R, R, R, R, R, R, R, R, R, R, R, R, R, R, R, R, R, R...

Especificando Método de Reamostragem

Antes de ajustar o modelo por meio da função train, é possível selecionar o método de reamostragem desejado no modelo a partir da função trainControl, que em seguida será dada como um argumento da primeira função.

Como padrão, o método usado é o bootstrap, no entanto, é possível usar outros métodos (caso queira saber algumas das opções e uma breve explicação delas coloquei no apêndice). Nesse exemplo, será utilizado a reamostragem Repeated 5-Fold Cross-Validation.

library(caret)
fitControl <- trainControl(## 5-fold CV
                           method = "repeatedcv",
                           number = 5,
                           ## 5 repetições
                           repeats = 5)

Ajustando Modelo com train

Agora que já foi definido o método de reamostragem podemos ajustar o modelo. O primeiro argumento da função train é uma fórmula contendo a variável de classificação e o preditores. Em seguida, especifica-se o tipo de modelo que deseja ajustar a partir do argumento method. Dessa forma, será ajustado um modelo Random Forest para tentar classificar a variável Class do banco de dados Sonar a partir dos preditores existentes. A sintaxe básica para ajustar esse modelo usando o método de reamostragem Repeated 5-Fold Cross-Validation é mostrada abaixo.

set.seed(13)
rf_fit <- train(Class ~ ., data = Sonar, 
                 method = "rf", 
                 trControl = fitControl)
rf_fit

## Random Forest 
## 
## 208 samples
##  60 predictor
##   2 classes: 'M', 'R' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold, repeated 5 times) 
## Summary of sample sizes: 167, 166, 167, 166, 166, 167, ... 
## Resampling results across tuning parameters:
## 
##   mtry  Accuracy   Kappa    
##    2    0.8413457  0.6773813
##   31    0.8222937  0.6396326
##   60    0.8058942  0.6061802
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.

O modelo Random Forest possui um único parâmetro de ajuste, o mtry, que representa o número de variáveis amostradas aleatoriamente como candidatas em cada divisão das árvores de decisões calculadas.

Os valores padrões testados nesse modelo estão representados na primeira coluna, e o modelo final é escolhido de acordo com o parâmetro que maximiza a métrica de desempenho, sendo nesse caso mtry=2 associado a acurácia de 0.84.

As colunas “Accuracy” e “Kappa” trazem as médias dessas métricas calculadas a partir da reamostrafem 5-Fold Cross_Validation repetida 5 vezes para cada um dos valores do parâmetro testados. Em modelos como esse, a função train cria automaticamente uma grade de parâmetros de ajuste, que, por padrão, tem tamanho 3p3p, sendo p o número de parâmetros em questão.

A função train possui outras funcionalidades/especificações que serão mostradas a seguir.

Notas sobre reprodutibilidade

Ao construir um modelo, os números aleatórios são utilizados nos índices de reamostragem mas também na fase de estimação dos parâmetros em alguns casos. Sendo assim, é importante haver maneiras de controlar a aleatoridade, a fim de permitir a reprodutibilidade dos modelos. A seguir estão as duas principais maneiras de garantir resultados reproduzíveis utilizando a função train.

• A primeira opção é fixar uma semente utilizando set.seed(semente) antes de chamar a função train.
• A opção alternativa é, quando deseja uma divisão específica dos dados, utilizar o argumento index dentro da função trainControl

Nos casos em que os modelos são criados dentro da reamostragem as sementes também podem ser definidas.

Embora a definição de uma semente antes de usar a função train garanta que os mesmos números aleatórios serão usados, é improvável que isso aconteça quando o processamento paralelo é utilizado. Nessa situação, o argumento seeds pode ser utilizado dentro da função trainControl, pelo qual é passado uma lista vetores usados como semente.

Vale ressaltar que a forma como os números aleatórios são utilizados depende muito do autor do pacote utilizado em cada um dos modelos, sendo importante pesquisar sobre isso.

Personalizando o Processo de Ajuste do Modelo

Opções de Pré-Processamento

Juntamente com a função train é possível informar, a partir do argumento preProcess, um vetor de strings contendo os métodos de pré-processamento que o usuário deseja aplicar, como centralização, escalonamento, imputação e entre outros. Além disso, outras opções podem ser informadas a partir da função trainControl.

Alterando Parâmetros de Ajuste do Modelo

A grade de parâmetros de ajuste testados no modelo pode ser especificado pelo usuário. Para isso basta adicionar o argumento tuneGrid á função train contendo um data frame com os valores de cada parâmetro nas colunas (os nomes das colunas devem ser os mesmos dos parâmetros do modelo a ser ajustado). Para construir esse data frame o usuário pode utilizar a funçaõ expand.grid, como mostrado a baixo. Dessa forma, o modelo será ajustado para cada combinação dos valores dos parâmetros(no caso em que o modelo tem mais de um parâmetro).

rfGrid <-  expand.grid(mtry = 2:8)
set.seed(13)
rf_fit2 <- train(Class ~ ., data = Sonar, 
                 method = "rf", 
                 trControl = fitControl, 
                 tuneGrid = rfGrid)
rf_fit2

## Random Forest 
## 
## 208 samples
##  60 predictor
##   2 classes: 'M', 'R' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold, repeated 5 times) 
## Summary of sample sizes: 167, 166, 167, 166, 166, 167, ... 
## Resampling results across tuning parameters:
## 
##   mtry  Accuracy   Kappa    
##   2     0.8480166  0.6910795
##   3     0.8373535  0.6700266
##   4     0.8431397  0.6810660
##   5     0.8317079  0.6585416
##   6     0.8326149  0.6603026
##   7     0.8366291  0.6688056
##   8     0.8365394  0.6682795
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.

Outra opção sem ser ajustar o modelo com os valores padrões ou informá-los manualmente é usar uma amostra aleatória de possíveis combinações de parâmetros de ajuste. A fim de utilizar uma pesquisa aleatória, basta utilizar o argumento search="random" ao chamar a função train. Nesse caso, pode-se adicionar o argumento tuneLength para definir o número total de combinações de parâmetros que devem ser avaliadas.

Função trainControl

Como visto anteriormente, a função trainControl controla a maneira como os modelos são criados, sendo possível informar diversos valores:

• method: especifica o método de reamostagrem, podendo assumir os seguintes valores: "boots" para Bootstrap, "cv" para K-Fold Cross Validation, "LOOCV" para Leave One Out Cross Validation, "LGOCV" para Leave Group Out Cross Validation, "repeatedcv" para Repeated K-Fold Cross Validation,"none" para ajustar apenas um modelo no banco informado, "oob" para estimativas Out of Bag e outros mais que você pode consultar no help da função ?trainControl. É importante dizer que nem todos modelos são compatíveis com todos métodos de reamostragem;
• number: número de grupos criados na reamostragem K-Fold Cross Validation ou número de interações de reamostragem usando Bootstrap ou Leave Group Out Cross Validation;
• repeats: número de repetições no método Repeated K-Fold Cross Validation;
• verboseIter: argumento lógico para imprimir log de treinamento.
• returnData: argumento lógico para salvar dados em uma ranhura chamada “trainingData”;
• p: para caso de Leave Group Out Cross Validation, porcentagem de treinamento;
• Para method = "timeslice", trainControl tem opções initialWindow, horizon e fixedWindow que controlam como a validação cruzada pode ser usada para dados de série temporal;
• classProbs: argumento lógico que determina se as probabilidades de classe devem ser calculadas para amostras retidas durante a reamostragem;
• index e indexOut: listas opcionais com elementos para cada iteração de reamostragem. Cada elemento da lista são as linhas de amostra usadas para treinamento naquela iteração ou que devem ser mantidas. Quando esses valores não são especificados, a função os gera;
• summaryFunction: função para calcular resumos de desempenho alternativos;
• selectionFunction: função para escolha dos parâmetros de ajuste ideais;
• returnResamp: string indicando quantas métricas de desempenho reamostradas devem ser salvar, pode assumir os valores: "final","all" e "none".;
• savePredictions: indicador de quanto das predições hold-out para cada reamostragem devem ser salvas. Os possíveis valor são "all"(equivalente a TRUE), "none"(equivalente a FALSE) e "final", que salva as predições dos parâmetros de ajuste ideais.
• allowParallel: argumento lógico que informa de função deve usar processamento paralelo.

A função abrange outras opções que podem ser consultadas a partir do seu help (?trainControl).

Métricas de Desempenho Alternativas

Como padrão, para problemas de regressão as métricas RMSE, R2R2 e o Erro Médio Absoluto são calculadas, enquanto que em problemas de classificação as métricas calculdas são a Acurácia e Kappa. Para a escolha dos parâmetros de ajuste ideais são usados o RMSE e a Acurácia, porém, utilizando o argumento metric dentro da função train, o usuário pode modificar a medida de desempenho analisada para escolher o parâmetro ótimo. Se nenhuma dessas métricas são satisfatórias, o usuário pode modificar os resumos de perfomance calculados a partir do argumento summaryFunction da função trailControl. O argumento deve conter uma função com alguns atributos obrigatórios. Essa função pode ser uma função pronta, como a twoClassSummary que será usada a seguir, ou uma criada pelo usuário, para saber mais sobre isso acesse aqui.

Como padrão, a função train avalia modelos de classificação a partir das classes preditas. No entanto, as probabilidades das classes também podem ser usadas para calcular medidas de desempenho. Para obtê-las,o argumento classProbs em trainControl deve ser definido como TRUE.

Ilustrando, iremos refazer o exemplo introdutório, mas agora utilizando a função twoClassSummary, que irá computar a sensibilidade, especificidade e área sob a curva ROC.

fitControl <- trainControl(method = "repeatedcv",
                           number = 5,
                           repeats = 5,
                           # estimar probabilidades das classes
                           classProbs = TRUE,
                           # avaliar performance utilizando função a seguir
                           summaryFunction = twoClassSummary)

set.seed(13)
rf_fit_3 <- train(Class ~ ., data = Sonar, 
                 method = "rf", 
                 trControl = fitControl, 
                 tuneGrid = rfGrid,
                 # especificando qual métrica deseja otimizar
                 metric = "ROC")
rf_fit_3

## Random Forest 
## 
## 208 samples
##  60 predictor
##   2 classes: 'M', 'R' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold, repeated 5 times) 
## Summary of sample sizes: 167, 166, 167, 166, 166, 167, ... 
## Resampling results across tuning parameters:
## 
##   mtry  ROC        Sens       Spec     
##   2     0.9383772  0.9260079  0.7587368
##   3     0.9354172  0.9095652  0.7547368
##   4     0.9338076  0.9205534  0.7542105
##   5     0.9358154  0.9007115  0.7524211
##   6     0.9288594  0.9006324  0.7544211
##   7     0.9291813  0.8989723  0.7648421
##   8     0.9292710  0.9042688  0.7586316
## 
## ROC was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.

Escolhendo Modelo Final

É possível modificar o algorítmo que seleciona os melhores valores dos parâmetros de ajuste. Como padrão, a função train escolhe o modelo com maior valor da métrica de desempenho principal como o modelo final (ou com o menor valor, no caso da medida de perfomance ser o Erro Quadrático Médio). Em contrapartida, a partir do argumento selectionFunction dentro da função train o usuário pode especificar uma função para determinar o modelo final. O pacote caret já abrange 3 funções: best que escolhe o modelo a partir do maior/menor valor da métrica, oneSE que se baseia na ideia da regra do erro padrão de Breiman et al (1984)(melhor descrita aqui) e tolerance que seleciona o modelo menos complexo dentro de uma tolerância percentual do melhor valor.

Extraindo previsões e probabilidades de classe

O objeto retornado pela função train possui um subobjeto chamado finalModel que contém o modelo final “otimizado”, aquele em que os parâmetros de ajuste proporcionaram a melhor métrica. É apartir dele que previsões em novos bancos de dados podem ser feitos. Quando vamos predizer a partir de um modelo, geralmente especificamos o argumento type. No caso da função predict aplicada a um objeto de classe train as opções do argumento type são padronizadas para ser raw ou prob. Como será mostrado no código abaixo, ao utilizar raw a função retorna a classe predita, enquanto que, ao usar prob a função retorna a probabilidade de cada nível do fator associado a cada elemento.

# nesse caso utilizaremos o mesmo banco de dados para calcular o predict apenas para demonstração
predict(rf_fit_3, newdata = Sonar[1:60], type = "raw") %>% head()

## [1] R R R R R R
## Levels: M R

predict(rf_fit_3, newdata = Sonar[1:60], type = "prob") %>% head()

##       M     R
## 1 0.174 0.826
## 2 0.204 0.796
## 3 0.250 0.750
## 4 0.166 0.834
## 5 0.176 0.824
## 6 0.170 0.830

Modelos

Após a apresentação do funcionamento da função train para o ajuste de modelos, iremos construir alguns modelos de Machine Learning utilizando o pacote caret. Para isso, será utilizado o banco de dados PimaIndiansDiabetes2 do pacote mlbench para solucionar o problema de classificação em questão. A base possui 8 atributos de mulheres com herança indígena do grupo Pima e a suas classsificações quanto ao resultado de teste para diabetes. Sendo assim, a ideia é predizer o resultado do teste de acordo com as observações de cada mulher. Cada modelo será ajustado em uma base treino e, em seguida, aplicado em uma base teste para calcular medidas de performance (usando a função definida abaixo). Para essa divisão, será utilizada a função createDataPartition do pacote caret, que permite a divisão do banco de dados com uma distribuição semelhante da variável fornecida (outcome).

data(PimaIndiansDiabetes2)
dados <- PimaIndiansDiabetes2 %>% na.omit()

set.seed(13)

split <- createDataPartition(dados$diabetes, p = .75, list = FALSE)
treino <- dados[ split,]
teste  <- dados[-split,]

metricas <- function(mod, classificacao, probs){

  labels <- as.factor(teste$diabetes)
  matriz_confusao <- confusionMatrix(classificacao,labels)
  acuracia<- round(as.numeric(matriz_confusao$overall[1]),3)
  sensibilidade <- round(as.numeric(matriz_confusao$byClass[1]),3)
  especificidade <- round(as.numeric(matriz_confusao$byClass[2]),3)
  auc <- pROC::roc(labels, probs)$auc %>% round(3)

  tabela <- data.frame(Acuracia = acuracia,
                       Sensibilidade = sensibilidade,
                       Especificidade = especificidade,
                       AUC = auc)

  return(tabela)
}

ponto_corte <- round(table(treino$diabetes)[2]/table(treino$diabetes)[1],3)

Regressão Logística

A Regressão Logística é uma técnica estatística utilizada em problemas de classificação, que tem como objetivo mensurar a probabilidade associada à ocorrência de determinado evento a partir dos valores de variáveis explicativas, que podem ser categóricas ou contínuas. Esse método é análogo à regressão linear, no entanto é utilizado quando a variável resposta é categórica, podendo ser binária (Regressão Logística Binomial) ou categórica ordenada/desordenada (Regressão Logística Ordinal/Multinomial) com mais de 2 níveis.

Nesse artigo será abordado exclusivamente o caso em que a variável resposta é binária. Um modelo de regressão logística ajusta o log da razão de chances, que nada mais é que a razão entre a probabilidade do seu evento de interesse (θiθi) e a probabilidade de não ocorrência desse evento (1−θi1−θi). Sendo assim, o modelo pode ser expresso por:

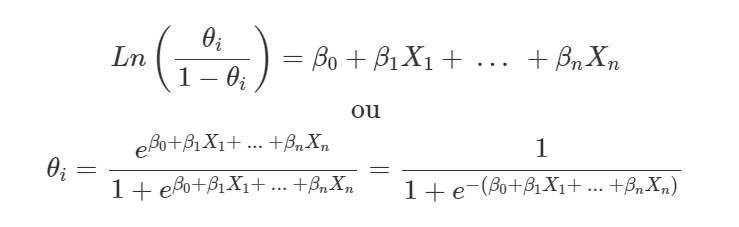
Como é possível notar na segunda expressão, a regressão logística utiliza a função logística para representar a relação entre a variável dependente e as preditoras. Dessa forma, os valores previstos assumem valores entre 0 e 1, que representam a probabilidade do evento de interesse. Diferentemente da regressão linear, nesse caso o método da máxima verossimilhança é utilizado para estimar os coeficientes do modelo.

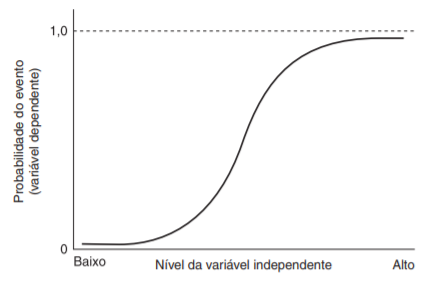
Por fim, a conclusão é de que a razão de chance indica proporcionalmente o quanto a ocorrência do evento de interesse é mais provável do que sua não ocorrência, isso de acordo com os valores das variáveis explicativas aplicados na expressão a baixo.

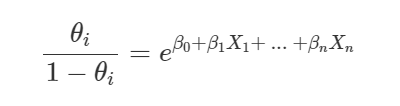
Após essa breve explicação da técnica, podemos ajustá-la a partir da função train do pacote caret, como mostrado no código a seguir.

set.seed(13)

modelo_glm <- train(
  diabetes ~ .,
  data = treino,
  method = "glm",
  family = "binomial",
  metric="ROC",
  trControl=trainControl(
    method = "cv",
    number = 5,
    classProbs = TRUE,
    summaryFunction = twoClassSummary,
    savePredictions = "final"
  )
)

modelo_glm

## Generalized Linear Model 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 237, 235, 237, 236, 235 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.8202271  0.8826923  0.5315789

summary(modelo_glm)

## 
## Call:
## NULL
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.7508  -0.6593  -0.3750   0.5927   2.6124  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -10.223330   1.435972  -7.119 1.08e-12 ***
## pregnant      0.030778   0.063286   0.486  0.62673    
## glucose       0.036761   0.006627   5.547 2.90e-08 ***
## pressure     -0.002526   0.013331  -0.189  0.84973    
## triceps       0.005621   0.019543   0.288  0.77363    
## insulin       0.001307   0.001641   0.796  0.42594    
## mass          0.085740   0.031805   2.696  0.00702 ** 
## pedigree      1.563650   0.500755   3.123  0.00179 ** 
## age           0.025787   0.020493   1.258  0.20828    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 375.08  on 294  degrees of freedom
## Residual deviance: 260.81  on 286  degrees of freedom
## AIC: 278.81
## 
## Number of Fisher Scoring iterations: 5

probs_glm <- predict(modelo_glm,teste, type = "prob")$pos
classificacao_glm <- as.factor(ifelse(probs_glm >= ponto_corte, "pos", "neg"))
metricas_glm <- metricas(modelo_glm,classificacao_glm,probs_glm)
metricas_glm

##   Acuracia Sensibilidade Especificidade   AUC
## 1    0.773         0.846          0.625 0.865

O código acima pode ser detalhado tendo em vista seus argumentos:

• a fórmula diabetes ~ . indica que estamos tentando predizer a variável diabetes a partir das demais variáveis do banco;
• a partir do argumento data informamos o banco em que será treinado o modelo;
• a fim de ajustar um modelo de regressão logística os argumentos method="glm" e family="binomial" foram utilizados;
• o ajuste dessa regressão logística não envolve parâmetros de melhoria do modelo, logo não foi utilizado o argumento tuneGrid nem a função expand.grid;
• o argumento metric="ROC" informa que a área sobre a curva ROC será usada para avaliar o melhor modelo;
• a função trainControlpassada ao argumento trControl especifica que o método de reamostragem 5-Fold Cross-Validation (method = "cv",number = 5) será utilizado, que outras medidas de resumo como especificidade e sensibilidade serão calculadas (summaryFunction = twoClassSummary) e outros detalhes.

Esse modelo construído possui todas variáveis explicativas do banco, sem avaliar se elas são significativas ou não. No entanto, o pacote caret também possui o método "glmStepAIC", que nada mais é do que o ajuste de uma regressão logística implementando o método Stepwise utilizando o Critério de Informação de Akaike para a seleção do melhor modelo. Nessa caso, no ajuste foi utilizado os argumentos method="glmStepAIC" e trace=FALSE, esse último que suprime as saídas automaticas ao rodar o código (cada iteração testada).

set.seed(13)

modelo_glm2 <- train(
  diabetes ~ .,
  data = treino,
  method = "glmStepAIC",
  family = "binomial",
  metric=c("ROC"),
  trControl=trainControl(
    method = "cv",
    number = 5,
    classProbs = TRUE,
    summaryFunction = twoClassSummary,
    savePredictions = "final"
  ),
  trace = FALSE
)

modelo_glm2

## Generalized Linear Model with Stepwise Feature Selection 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 237, 235, 237, 236, 235 
## Resampling results:
## 
##   ROC       Sens       Spec     
##   0.837833  0.8929487  0.5421053

summary(modelo_glm2)

## 
## Call:
## NULL
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.8644  -0.6582  -0.3821   0.6181   2.6545  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -10.593366   1.320332  -8.023 1.03e-15 ***
## glucose       0.039101   0.005925   6.600 4.12e-11 ***
## mass          0.091169   0.024402   3.736 0.000187 ***
## pedigree      1.559613   0.493892   3.158 0.001590 ** 
## age           0.032201   0.014796   2.176 0.029528 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 375.08  on 294  degrees of freedom
## Residual deviance: 261.82  on 290  degrees of freedom
## AIC: 271.82
## 
## Number of Fisher Scoring iterations: 5

probs_glm <- predict(modelo_glm2,teste, type = "prob")$pos
classificacao_glm <- as.factor(ifelse(probs_glm >= ponto_corte, "pos", "neg"))
metricas_glm <- metricas(modelo_glm2,classificacao_glm,probs_glm)
metricas_glm

##   Acuracia Sensibilidade Especificidade   AUC
## 1    0.794         0.862          0.656 0.869

A fim de calcular a importância de cada variável no modelo de regressão logística pode-se utilizar a função varImp, que fornece uma medida de importância a partir do valor absoluto da estatística-t para cada parâmetro do modelo.

importancia_var <- varImp(modelo_glm) 

ggplot(importancia_var) +
  labs(title = "Importância das Variáveis", y = "Importância", x ="Variáveis")

Random Forest

O Random Forest é um algoritmo de aprendizado de máquinas supervisionado, usado em problemas de classificação e regressão, pautado em 2 técnicas principais: a de árvores de decisão e a de bagging, ou boostrap aggregating.

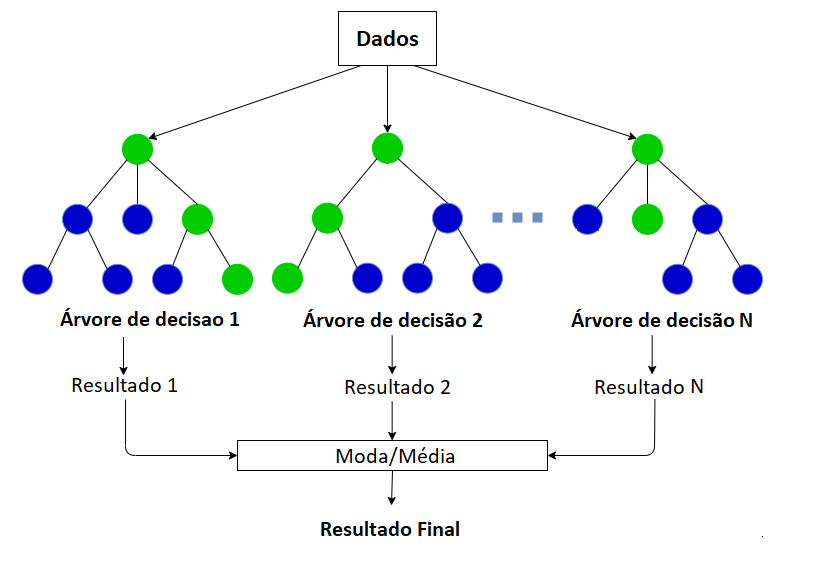
O algoritmo consiste na construção de um número grande de árvores de decisão não correlacionadas, que no final serão usadas para a construção de um modelo final. Por ser um método ensemble, ou seja, que combina diferentes modelos para a obtenção de um modelo final, é um algoritmo mais robusto e complexo, exigindo maior tempo computacional, mas geralmente alcançando melhores resultados.

O primeiro passo do algoritmo é criar, aleatoriamente, amostras do banco de dados. Nesse processo, é utilizado o método de reamostragem bootstrap, em que são seleciconadas amostras com reposição dos elementos.

A partir disso, para cada amostra criada, uma árvore de decisão é modelada. No caso do modelo Random Forest, nem todas variáveis são consideradas para a divisão de um nó, o que é feito é a seleção aleatória de m variáveis (parâmetro mtry ao modelar com train), que são testadas para verificar qual será a melhor para a separação do nó.

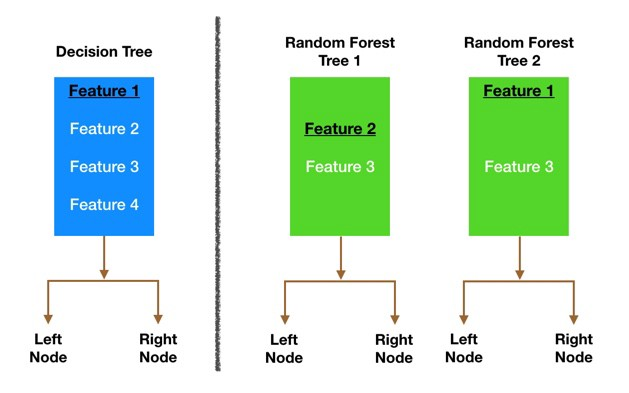
Este processo se repete na construção de todas as árvores para as diferentes amostras, garantindo aleatoridade durante a construção do modelo e a redução da correlação entre as árvores construídas. Uma vez que todas árvores foram modeladas, calcula-se uma predição final tendo como base as predições de todas as árvores, por isso o termo agregating. Essa predição é ponderada pelo erro preditivo de cada árvore, ou seja, árvores com menor erro preditivo têm mais peso na decisão.

Utilizando a função train do pacote caret é possível ajustar o modelo random forest a partir do código a seguir:

set.seed(13)

modelo_random_forest <- train(
  diabetes ~ .,
  data = treino,
  method = "rf",
  tuneGrid = expand.grid(mtry=2:8),
  metric="ROC",
  trControl=trainControl(
    method = "cv",
    number = 5,
    classProbs = TRUE,
    summaryFunction = twoClassSummary,
    savePredictions = "final"
  )
)

modelo_random_forest

## Random Forest 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 237, 235, 237, 236, 235 
## Resampling results across tuning parameters:
## 
##   mtry  ROC        Sens       Spec     
##   2     0.8284853  0.8930769  0.5610526
##   3     0.8193524  0.8879487  0.5515789
##   4     0.8170329  0.8828205  0.5621053
##   5     0.8212117  0.8930769  0.5621053
##   6     0.8290452  0.8779487  0.6036842
##   7     0.8242304  0.8779487  0.5831579
##   8     0.8208794  0.8778205  0.5936842
## 
## ROC was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 6.

probs_rf <- predict(modelo_random_forest,teste, type = "prob")$pos
classificacao_rf <- as.factor(ifelse(probs_rf >= ponto_corte, "pos", "neg"))
metricas_rf <- metricas(modelo_random_forest,classificacao_rf,probs_rf)
metricas_rf

##   Acuracia Sensibilidade Especificidade   AUC
## 1    0.804         0.862          0.688 0.875

Detalhando o código, temos que:

• a fórmula diabetes ~ . indica que estamos tentando predizer a variável diabetes a partir das demais variáveis do banco;
• a partir do argumento data informamos o banco em que será treinado o modelo;
• a fim de ajustar um modelo Random Forest o argumento method="rf" foi utilizado;
• os parâmetros de ajuste que serão testados foram especificados no argumento tuneGrid a partir da função expand.grid;
• o argumento metric="ROC" informa que a área sobre a curva ROC será usada para avaliar o melhor modelo/parâmetro de ajuste;
• a função trainControlpassada ao argumento trControl especifica que o método de reamostragem 5-Fold Cross-Validation (method = "cv",number = 5) será utilizado, que outras medidas de resumo como especificidade e sensibilidade serão calculadas (summaryFunction = twoClassSummary) e outros detalhes.

Por ser um modelo ensemble o random forest não tem uma interpretação clara como na árvore de decisão, no entanto é possível calcular uma medida de importância de cada variável no modelo final utilizando a função varImp. Essa medida é baseada na redução da soma de quadrados dos resíduos de cada divisão e te permite uma análise de quais variáveis são mais importantes na classificação, podendo ser usada para seleção de variáveis para outros modelos.

importancia_var <- varImp(modelo_random_forest) 

ggplot(importancia_var) +
  labs(title = "Importância das Variáveis",y = "Importância", x ="Variáveis")

Support Vector Machine

Support Vector Machine(SVM), ou Máquina de Vetores de Suporte, é uma técnica de aprendizado supervisionado utilizado em problemas de classificação e regressão, e para detectação de outliers. A ideia é que, a partir de um banco treino, o algoritmo reconheça padrões das variáveis presentes no modelo e construa uma separação no espaço entre as duas possíveis classificações dos elementos. Dessa forma, o SVM toma como entrada um novo elemento e consegue predizer sua classe, o que o faz um classificador linear não-probabilístico.

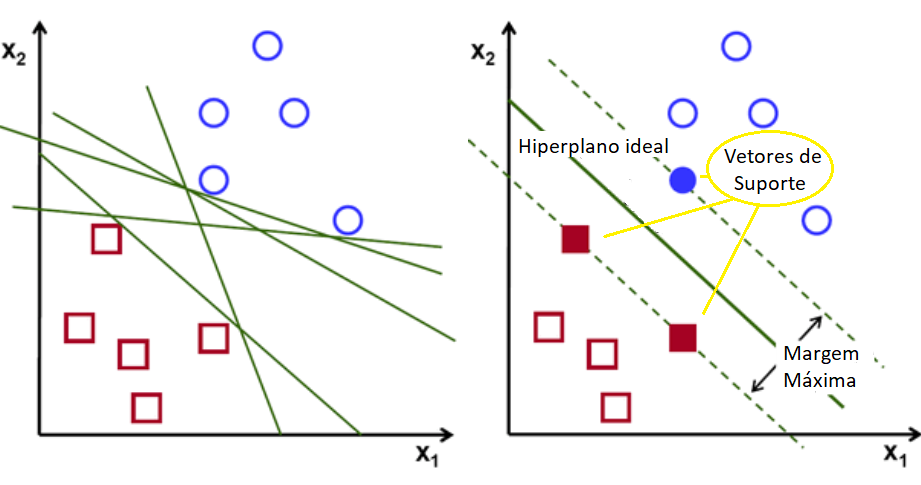
Sendo assim, o objetivo do algoritmo é encontrar um hiperplano, em um espaço N dimensional(sendo N o número de variáveis presentes no modelo), que separe os dados de acordo com suas classificações. No entanto, existem vários hiperplanos que dividem os dados pela sua classe. A ideia é encontrar o hiperplano com uma divisão tão ampla quanto possível, ou seja, que possui a margem máxima, fornecendo, assim, algum reforço para que os pontos de dados futuros possam ser classificados com maior confiança. Vale ressaltar que é possível encontrar uma divisão perfeita para as classes, porém isso não implica em poder preditivo. Assim como em uma regressão nós evitamos o overfitting, nesse caso o ideal é um hiperplano que promova uma divisão generalizada.

Os vetores de suporte são os pontos que estão mais próximos do hiperplano, sendo responsáveis pela posição e inclinação dele. Usando esses vetores é que maximizamos a margem, que, por definição, é a distância entre o vetor de suporte e o hiperplano. Sendo assim, são os vetores de suporte que auxiliam na construção do hiperplano, de forma que as previsões dependem apenas deles, e não do conjunto de treinamento.

Quando os dados são linearmente separáveis o modelo usado é o SVM Linear com margens rígidas, entretanto a maioria das separações exigem soluções mais complexas.

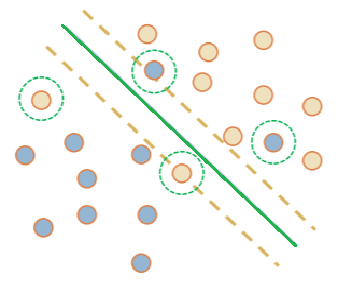
Nos casos em que os dados não são linearmente separáveis devido a presença de ruídos/outiliers é utilizado o modelo SVM Linear com margens suaves. Nesse caso, é permitido que alguns dados violem a restrição do hiperplano, o que é controlado por uma constante C de penalização das imprecisões na divisão.

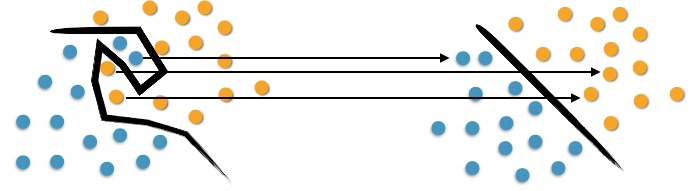
Há ainda os problemas resolvidos a partir do SVM Não Linear, quando é necessário mapear o conjunto de treinamento de seu espaço original (não linear) para um novo espaço de maior dimensão, denominado espaço de características (feature space), que é linear. Para a transformação das variáveis são utilizadas funções matemáticas chamadas de Kernels, e, como consequência, o modelo terá um parâmetro sigma que representa a intesidade da transformação dos dados.

No exemplo abaixo o modelo SVM construído utiliza tanto a constante C, para a penalização das imprecisões na divisão, quanto o valor sigma para representar a intesidade da transformação dos dados.

set.seed(13)

modelo_svm <- train(
  diabetes ~ .,
  data = treino,
  method = "svmRadial",
  tuneLength = 5,
  metric="ROC",
  trControl=trainControl(
    method = "cv",
    number = 5,
    classProbs = TRUE,
    summaryFunction = twoClassSummary,
    savePredictions = "final"
  )
)

modelo_svm

## Support Vector Machines with Radial Basis Function Kernel 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 237, 235, 237, 236, 235 
## Resampling results across tuning parameters:
## 
##   C     ROC        Sens       Spec     
##   0.25  0.8034821  0.8367949  0.6136842
##   0.50  0.8026646  0.8725641  0.5431579
##   1.00  0.7892797  0.8828205  0.4915789
##   2.00  0.7703337  0.8726923  0.4494737
##   4.00  0.7644983  0.8778205  0.4073684
## 
## Tuning parameter 'sigma' was held constant at a value of 0.1250316
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were sigma = 0.1250316 and C = 0.25.

probs_svm <- predict(modelo_svm,teste, type = "prob")$pos
classificacao_svm <- as.factor(ifelse(probs_svm >= ponto_corte, "pos", "neg"))
metricas_svm <- metricas(modelo_svm,classificacao_svm,probs_svm)
metricas_svm

##   Acuracia Sensibilidade Especificidade   AUC
## 1    0.784         0.831          0.688 0.852

O código acima pode ser detalhado com respeito aos seus argumentos da seguinte forma:

• a fórmula diabetes ~ . indica que estamos tentando predizer a variável diabetes a partir das demais variáveis do banco;
• a partir do argumento data informamos o banco em que será treinado o modelo;
• a fim de ajustar um modelo SVM o argumento method="svmRadial" foi utilizado;
• nesse caso optou-se por não especificar os parâmetros de ajuste, mas, caso queira, basta especificá-los no argumento tuneGrid a partir da função expand.grid;
• o argumento metric="ROC" informa que a área sobre a curva ROC será usada para avaliar o melhor modelo/parâmetro de ajuste;
• a função trainControlpassada ao argumento trControl especifica que o método de reamostragem 5-Fold Cross-Validation (method = "cv",number = 5) será utilizado, que outras medidas de resumo como especificidade e sensibilidade serão calculadas (summaryFunction = twoClassSummary) e outros detalhes.

Assim como no modelo Random Florest, a técnica de SVM não possui uma interpretação clara da relação das variáveis com a conclusão do ajuste. Sendo assim, também é possível usar a função varImp para avaliar a importância de cada variável no modelo.

importancia_var <- varImp(modelo_svm) 

ggplot(importancia_var) +
  labs(title = "Importância das Variáveis", y = "Importância", x ="Variáveis")

Pacote caret Ensemble

Além do pacote caret, existe o pacote caretEnsemble, que permite a criação de ensembles utilizando modelos construídos pelo caret.

caretList

A função caretList desse pacote permite a criação de vários modelos utilizando o mesmo banco de dados e os mesmos parâmetros de reamostragem. Ela praticamente possui os mesmos argumentos da função train.

Existem duas maneiras de especificar quais modelos você deseja ajustar utilizando essa função.Na primeira forma, basta informar a partir do argumento methodList um vetor de caracteres contendo os modelos que serão ajustados, utilizando os parâmetros padrões da função train.

set.seed(13)

modelos_methodList <- caretEnsemble::caretList(
  diabetes ~ .,
  data = treino,
  metric=c("Accuracy","ROC"),
  trControl=trainControl(
    method = "cv",
    number = 5,
    classProbs = TRUE,
    summaryFunction = twoClassSummary,
    savePredictions = "final"
  ),
  methodList=c("glm", "rf","svmRadial")
)

modelos_methodList

## $glm
## Generalized Linear Model 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 236, 236, 236, 236, 236 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.8299055  0.8932051  0.5715789
## 
## 
## $rf
## Random Forest 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 236, 236, 236, 236, 236 
## Resampling results across tuning parameters:
## 
##   mtry  ROC        Sens       Spec     
##   2     0.8117679  0.8580769  0.5615789
##   5     0.8004184  0.8529487  0.5615789
##   8     0.7976721  0.8578205  0.5915789
## 
## ROC was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.
## 
## $svmRadial
## Support Vector Machines with Radial Basis Function Kernel 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 236, 236, 236, 236, 236 
## Resampling results across tuning parameters:
## 
##   C     ROC        Sens       Spec     
##   0.25  0.8128070  0.8379487  0.6121053
##   0.50  0.8102159  0.8733333  0.5710526
##   1.00  0.7969501  0.8633333  0.4905263
## 
## Tuning parameter 'sigma' was held constant at a value of 0.116309
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were sigma = 0.116309 and C = 0.25.
## 
## attr(,"class")
## [1] "caretList"

Com a outra alternativa, utilizando o argumento tuneList, é possível personalizar como cada modelo será construído. Para isso, basta indicar uma lista dos modelos definidos a partir da função caretModelSpec, no qual você especifica o modelo a ser construído e outras informações, como mostrado abaixo.

set.seed(13)

modelos_tuneList <-  caretEnsemble::caretList(
  diabetes ~ .,
  data = treino,
  metric=c("Accuracy","ROC"),
  trControl=trainControl(
    method = "cv",
    number = 5,
    classProbs = TRUE,
    summaryFunction = twoClassSummary,
    savePredictions = "final"
  ),
  tuneList = list(
    glm = caretEnsemble::caretModelSpec(
      method = "glm",
      family = "binomial"
    ),
    rf = caretEnsemble::caretModelSpec(
      method = "rf",
      tuneGrid = expand.grid(
        mtry = 2:8
      )
    ),
    svm = caretEnsemble::caretModelSpec(
      method = "svmRadial",
      tuneLength = 5
      )
    )
)

modelos_tuneList

## $glm
## Generalized Linear Model 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 236, 236, 236, 236, 236 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.8299055  0.8932051  0.5715789
## 
## 
## $rf
## Random Forest 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 236, 236, 236, 236, 236 
## Resampling results across tuning parameters:
## 
##   mtry  ROC        Sens       Spec     
##   2     0.8080634  0.8528205  0.5415789
##   3     0.8078036  0.8529487  0.5715789
##   4     0.8021491  0.8578205  0.5615789
##   5     0.8046188  0.8528205  0.5721053
##   6     0.8008198  0.8529487  0.5715789
##   7     0.7992510  0.8580769  0.5915789
##   8     0.8004521  0.8629487  0.5915789
## 
## ROC was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.
## 
## $svm
## Support Vector Machines with Radial Basis Function Kernel 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 236, 236, 236, 236, 236 
## Resampling results across tuning parameters:
## 
##   C     ROC        Sens       Spec     
##   0.25  0.8091903  0.8328205  0.6321053
##   0.50  0.8063225  0.8833333  0.5405263
##   1.00  0.7918219  0.8582051  0.5005263
##   2.00  0.7693995  0.8532051  0.4500000
##   4.00  0.7531444  0.8732051  0.3389474
## 
## Tuning parameter 'sigma' was held constant at a value of 0.1386857
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were sigma = 0.1386857 and C = 0.25.
## 
## attr(,"class")
## [1] "caretList"

Em ambos casos é possível acessar cada modelo separadamente utilizando lista_modelos$nome_modelo_especifico.

modelos_methodList$glm

## Generalized Linear Model 
## 
## 295 samples
##   8 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 236, 236, 236, 236, 236 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.8299055  0.8932051  0.5715789

É relevante ressaltar a importância de, ao utilizar a função caretlist, especificar explicitamente os índices de reamostragem a partir do argumento index=createResample(variável resposta, number).Isso se deve ao fato de que a função caretList tentará definir os índices automaticamente, mas como não é uma garantia de sucesso, é uma boa prática definí-los “manualmente”. A garantia de que os modelos serão construídos utilizando os mesmos índices é essencial principalmente caso você vá realizar um ensemble com essa lista de modelos.

caretEnsemble

A função caretEnsemble usa como método o glm para criar uma junção linear simples dos modelos. Um conjunto de modelos é um bom candidato para realizar o ensemble quando eles são não correlacionados mas possuem AUCs similares.

Para checar a correlação entre modelos basta usar a função modelCor juntamente com a função resamples, ambas do pacote caret. Nesse caso, como você pode ver abaixo, os modelos são fortemente correlacionados, mas ainda assim será feito a demonstração do ajuste do ensemble utilizando a lista de modelos modelos_methodList construída anteriormente (também seria possível realizar o ensemble utilizando modelos_tuneList).

modelCor(resamples(modelos_methodList))

##                 glm        rf svmRadial
## glm       1.0000000 0.9571054 0.8905367
## rf        0.9571054 1.0000000 0.9599987
## svmRadial 0.8905367 0.9599987 1.0000000

ensemble_methodList <- caretEnsemble::caretEnsemble(
  modelos_methodList,
  metric=c("Accuracy","ROC"),
  trControl=trainControl(
    classProbs = TRUE,
    summaryFunction = twoClassSummary,
    savePredictions = "final"
  ))

summary(ensemble_methodList)

## The following models were ensembled: glm, rf, svmRadial 
## They were weighted: 
## 2.4387 -4.6363 -1.7467 1.4803
## The resulting ROC is: 0.7924
## The fit for each individual model on the ROC is: 
##     method       ROC      ROCSD
##        glm 0.8299055 0.04838357
##         rf 0.8117679 0.06767155
##  svmRadial 0.8128070 0.06113376

Nesse caso o ensemble não provocou uma melhora no AUC, mas em muitos casos pode obter melhores resultados.

caretStack

A função caretStack te permite criar combinações lineares ou não lineares de modelos construídos a partir da função train, criando um modelo final por qualquer método compatível com o pacote caret.

ensemble_caret_stack <- caretEnsemble::caretStack(modelos_tuneList,
                                   method='glmnet',
                                   metric="ROC",
                                   trControl=trainControl(
                                      classProbs = TRUE,
                                      summaryFunction = twoClassSummary,
                                      savePredictions = "final")
                                   )

ensemble_caret_stack

## A glmnet ensemble of 3 base models: glm, rf, svm
## 
## Ensemble results:
## glmnet 
## 
## 295 samples
##   3 predictor
##   2 classes: 'neg', 'pos' 
## 
## No pre-processing
## Resampling: Bootstrapped (25 reps) 
## Summary of sample sizes: 295, 295, 295, 295, 295, 295, ... 
## Resampling results across tuning parameters:
## 
##   alpha  lambda        ROC        Sens       Spec     
##   0.10   0.0005156076  0.8195073  0.9000747  0.5525236
##   0.10   0.0051560761  0.8258995  0.8979155  0.5491325
##   0.10   0.0515607609  0.8294884  0.8951631  0.5322594
##   0.55   0.0005156076  0.8196377  0.9000747  0.5513472
##   0.55   0.0051560761  0.8261570  0.8961992  0.5459692
##   0.55   0.0515607609  0.8290138  0.9054762  0.5174190
##   1.00   0.0005156076  0.8193522  0.8999857  0.5522871
##   1.00   0.0051560761  0.8268405  0.8972662  0.5510250
##   1.00   0.0515607609  0.8298327  0.9098405  0.4991226
## 
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were alpha = 1 and lambda = 0.05156076.

Curiosidade

O pacote caret é um dos pacotes mais populares para modelagem preditiva e aprendizado supervisionado. Isso porque o pacote fornece uma interface consistente para todos os recursos de aprendizado de máquina mais poderosos do R. Como curiosidade, é possível comparar o número de downloads do pacote caret com outros pacotes também utilizados para ajustar modelos de machine learning. Dessa forma, no gráfico abaixo, é possível reparar que desde de sua criação, em 2016, o caretfoi o pacote com mais downloads comparado com algumas outras opções presentes no R.

library(dlstats)

x <- cran_stats(c("caret","tidymodels","randomForest","recipes","ranger","xgboost","caretEnsemble"))

if (!is.null(x)) {
  head(x)
  ggplot(x, aes(end, downloads, group=package, color=package)) +
    geom_line() + geom_point(aes(shape=package))+
    labs(x="Data",y="Downloads",title = "Número de downloads ao longo do tempo \n de alguns pacotes usados em Machine Learning")
}