O que são Modelos Lineares Generalizados?

A Análise de Regressão Linear era considerada a principal técnica de modelagem estatística até meados do século XX. Seu principal objetivo é analisar a relação entre uma variável resposta e uma ou mais variáveis explicativas, para identificar uma função que a descreva.

Através dela é possível entender as causas de variação de um fenômeno e predizer seu comportamento de acordo com as variáveis explicativas. Quando se tem apenas uma variável explicativa, a regressão é simples. Do contrário, tem-se uma regressão múltipla.

Apesar de poderosa, a Análise de Regressão Linear exige fortes suposições para sua utilização, como normalidade, independência e homoscedasticidade dos erros. Foi a partir dessas limitações que surgiram os Modelos Lineares Generalizados.

O conceito

Os MLGs (Modelos Lineares Generalizados) são uma extensão dos modelos de regressão simples e múltipla.
Eles possibilitam utilizar outras distribuições para os erros e uma função de ligação relacionando a média da variável resposta à combinação linear das variáveis explicativas.

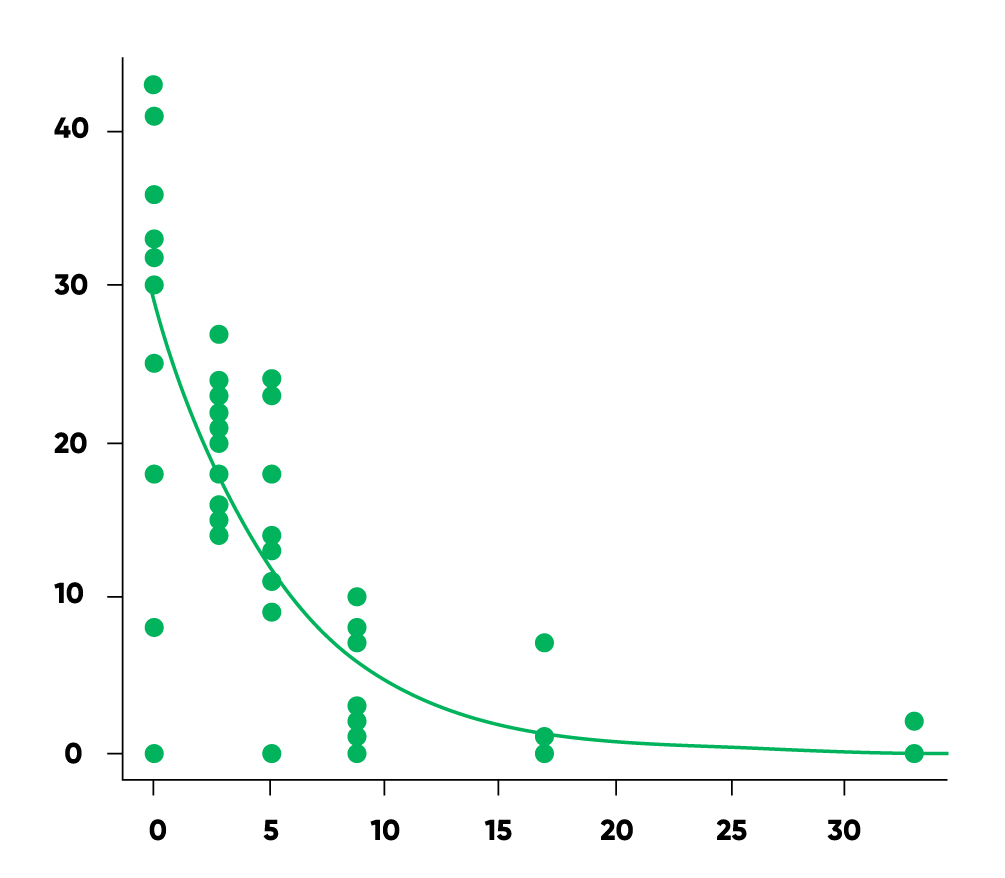
Os Modelos Lineares Generalizados permitem, portanto, ‘alargar’ as suposições admitidas e examinar não somente as relações lineares entre as variáveis explicativas e a resposta.

Geralmente em um problema de modelagem envolvendo MLG, deve-se definir:
• o comportamento (distribuição) da variável resposta;
• as variáveis explicativas;
• a função de ligação que irá ligar as variáveis explicativas à variável resposta.

Com os modelos lineares generalizados é possível modelar variáveis de interesse que assumem a forma de contagem, contínuas simétricas e assimétricas, binárias e categóricas.

Uma das limitações dos MLGs é a exigência de que os erros sejam independentes. Isso significa que eles não são capazes de modelar bancos de dados com estruturas longitudinais (amostras medidas mais de uma vez ao longo do tempo), espaciais ou multiníveis. Mas é possível contornar essa fraqueza utilizando Modelos Lineares Generalizados Mistos ou Equações de Estimações Generalizadas.

Algumas regressões admitidas pela classe de Modelos Lineares Generalizados

Abaixo, listamos as principais distribuições exigidas pela classe MLGs, e o tipo de dado que cada uma delas modela:

1. Regressão de Poisson

As regressões de Poisson são usadas para modelar dados de contagem, por exemplo, o número de mortes em determinada região ou o número de consumidores que entram em um estabelecimento comercial.

Normalmente, é utilizada uma função de ligação logarítmica para relacionar a variável resposta às variáveis explicativas. Essa função é muito importante para essas regressões, pois impede o surgimento de resultados negativos e fornece boas interpretações a partir do exponencial dos coeficientes.

Quando a contagem está sujeita a uma população e o número de eventos for pequeno em relação ao tamanho da população, acrescenta-se um offset às regressões de Poisson e, caso contrário, utiliza-se a regressão binomial logística.

Em modelos de Poisson é comum a presença de superdispersão, sendo que, quando presente no modelo, se faz necessário utilizar uma variância robusta ou migrar para modelos como a Binomial Negativa.

2. Regressão de Bernoulli / Regressão Logística

A regressão de Bernoulli é utilizada na modelagem de fenômenos que podem ser resumidos em uma variável binária, ou seja, se ocorreu ou não um evento. Quando se escolhe a função de ligação ‘logit’, ela passa a ser chamada de regressão logística.

Essa função é bastante utilizada pois, além de ser própria para dados binários auxiliando na tomada de decisões do tipo “Sim” ou “Não”, permite que sejam feitas interpretações a partir de Odds Ratios (Razões de Chances).

A regressão logística é muito utilizada em modelos de concessão de crédito, onde a partir de informações oferecidas pelo solicitante, a instituição financeira decide pela liberação ou não do crédito. Também é frequentemente utilizada em pesquisas clínicas que tem como objetivo verificar os fatores de influência na ocorrência ou não de uma determinada doença.

3. Regressão Gama

A regressão Gama é usada para modelar dados positivos e assimétricos. Enquanto a regressão de Poisson trata de modelar variáveis de contagem, ou seja, discretas, a regressão Gama modela variáveis contínuas. Normalmente também se utiliza a função de ligação logarítmica pelas mesmas razões já apresentadas na regressão de Poisson.

Pode-se utilizar esse tipo de modelo, por exemplo, para estudar os fatores que influenciam no valor de um imóvel (como sua condição, localização, área construída, etc.) ou ainda os fatores que influenciam na demanda de produtos em diferentes centros de distribuição.

Como se pôde ver, a classe de Modelos Lineares Generalizados é uma ferramenta poderosa que supera as limitações dos modelos de regressão linear e possibilita a resolução de muitos problemas, das mais diversas áreas do conhecimento.

Detalharemos em futuros posts, exemplos de aplicações de regressão de Poisson, Logística e Gama. Por isso, siga-nos nas redes sociais para saber quando saem os próximos artigos.