Esse artigo foi feito com a colaboração de Luis Henrique Velasquez
Machine Learning (ou aprendizado de máquina) é uma inteligência artificial que permite que computadores tomem decisões com a ajuda de algoritmos. Esses algoritmos reconhecem padrões e se tornam capazes de fazer predições. De forma bem simples, o Machine Learning se baseia na construção e no uso de algoritmos que “aprendem” a partir dos dados.
Falamos que uma máquina “aprende” com os dados quando ela consegue melhorar seu desempenho com o aumento de informação recebida. Dessa forma, utilizam-se observações e soluções calculadas anteriormente para realizar previsões de problemas utilizando dados distintos dos já observados.
É importante salientar que problemas como “escolher o aluno com a maior nota de Estatística da turma” ou “Verificar o produto mais recorrente dentre as compras dos clientes de um supermercado” não se tratam de problemas da área do Machine Learning. Esses problemas não utilizam dados para fazer previsões, eles podem ser resolvidos apenas utilizando a ordenação dos dados.
Os problemas de Machine Learning são divididos em três subáreas principais:
- Classificação: baseia-se em prever a categoria de uma observação dada. Aqui, procura-se estimar um “classificador” que gere como saída a classificação qualitativa de um dado não observado com base em dados de entrada (que abrangem observações com classificações já definidas).
Exemplo: um classificador que utilize dados não observados de um paciente e classifique-o como doente ou não-doente. - Regressão: de forma similar a classificação, utiliza dados de entrada (preditores) já observados para prever uma resposta. A grande diferença é que, neste caso, procura-se estimar um valor numérico e não uma classificação de uma observação.
Exemplo: estimar um modelo que utilize a idade e os anos de escolaridade de um indivíduo não-observado anteriormente para tentar prever seu salário. Utiliza-se como base desse modelo: idades, anos de escolaridades e salários de diversos indivíduos já observados anteriormente. - Agrupamento: também conhecido como “Clustering”, tem como objetivo agrupar observações em grupos conhecidos como “clusters”. Essas observações apresentam similaridades dentro de seu cluster e diferenças em relação aos demais clusters formados. Diferente da Classificação, não é realizada a rotulação dos clusters, fazendo com que não exista uma clusterização errada ou certa. A clusterização utilizada resulta em diferentes tipos de clusters, e a escolha dessas técnicas deve ser previamente analisada pelo pesquisador.
Exemplo: agrupar fotos de animais similares em clusters, sem ter o conhecimento prévio de qual animal está sendo apresentado.
Essas três subáreas podem ser divididas em dois tipos de aprendizado:
- Supervised Learning: ou “aprendizado supervisionado”, abrange as subáreas da Classificação e Regressão. Utiliza dados já observados que possuem respostas ou classificações rotuladas, possibilitando comparar as previsões das respostas/rótulos com os rótulos reais.
- Unsupervised Learning: ou “aprendizado não-supervisionado”, é onde a subárea do Clustering se encaixa. Suas técnicas não necessitam rótulos de suas observações e seu objetivo principal é encontrar grupos onde suas observações apresentem comportamento similar.
Medidas de Desempenho
Após entendermos a ideia básica de Machine Learning, talvez uma das principais dúvidas que encontramos é “como saber a qualidade do modelo que estou utilizando?” .
Isso dependerá do objetivo da técnica que iremos utilizar: Classificação, Regressão ou Clustering.
Classificação
Para a classificação, a acurácia e o erro são as medidas básicas de desempenho. Quanto maior a acurácia do modelo, maior serão os acertos e menores serão os erros cometidos. Ela pode ser calculada da seguinte forma:

Porém, o uso apenas de Acurácia e Erro podem não ser suficientes para avaliar o desempenho do modelo. Por exemplo, vamos considerar que construímos um modelo com 100 pacientes que classificou corretamente 98 pacientes como não-doentes e errou ao classificar dois indivíduos doentes, classificando-os também como “não-doentes”. Embora a acurácia desse modelo pareça muito boa (98%), vemos que ele errou a previsão de todos os casos positivos da doença!
Para avaliarmos nosso modelo de forma mais detalhada, utilizamos a Matriz de Confusão (“Confusion Matrix”). Nela, utilizamos classificação binária (Sim ou Não) dos rótulos do modelo e dos dados reais observados. Dessa forma, ao utilizarmos o modelo de classificação em dados já observados, conseguimos verificar o quanto que o modelo conseguiu predizer corretamente. A Matriz de Confusão é composta por 4 valores:
- True Positive (TP): Valores classificados como positivos nos dados originais e corretamente previstos como positivos no modelo.
- True Negatives (TN): Valores classificados como negativos nos dados originais e corretamente previstos como negativos no modelo.
- False Positives (FP): Valores classificados como negativos nos dados originais e erroneamente previstos como positivos no modelo.
- False Negatives (FN): Valores classificados como positivos nos dados originais e erroneamente previstos como negativos no modelo.

A partir desses valores, podemos calcular dois valores adicionais a Acurácia do modelo e que também servem para medir o desempenho da classificação:

O código abaixo ensina como calcular essas estatísticas a partir de uma matriz de confusão já conhecida.
# Construindo uma matriz de confusão (Confusion Matrix)
Conf <- matrix(c(212,53,78,371),nrow=2,ncol=2)
colnames(Conf) <- c(1,0)
rownames(Conf) <- c(1,0)
Conf## 1 0
## 1 212 78
## 0 53 371# Calculando o TP, FN, FP e TN
TP <- Conf[1, 1] # 212
FN <- Conf[1, 2] # 78
FP <- Conf[2,1] # 53
TN <- Conf[2,2] # 371
# Cálculo da Acurácia
acc <- (TP + TN)/(TP+TN+FP+FN)
acc # 81,65 %## [1] 0,8165266# Calculo da precisão
prec <- TP/(TP+FP)
prec # 80 %## [1] 0,8# Calculo Recall
rec <- TP/(TP+FN)
rec # 73,1 %## [1] 0,7310345Regressão
Para avaliarmos a qualidade do modelo de Regressão, usualmente utilizamos o RMSE (Raiz do Erro Quadrático Médio). O RMSE representa a distância média entre as previsões e a linha de regressão. Quanto maior o RMSE do modelo, menor é o seu desempenho, já que valores altos indicam maior quantidade de erros de predição.

No código abaixo, usaremos o banco de dados “air” para obter o RMSE de um modelo a partir da função “lm()” no R:
summary(air) # Verificando os dados freq angle ch_length velocity
Min. : 200 Min. : 0,000 Min. :0,0254 Min. :31,70
1st Qu.: 800 1st Qu.: 2,000 1st Qu.:0,0508 1st Qu.:39,60
Median : 1600 Median : 5,400 Median :0,1016 Median :39,60
Mean : 2886 Mean : 6,782 Mean :0,1365 Mean :50,86
3rd Qu.: 4000 3rd Qu.: 9,900 3rd Qu.:0,2286 3rd Qu.:71,30
Max. :20000 Max. :22,200 Max. :0,3048 Max. :71,30
thickness dec
Min. :0,0004007 Min. :103,4
1st Qu.:0,0025351 1st Qu.:120,2
Median :0,0049574 Median :125,7
Mean :0,0111399 Mean :124,8
3rd Qu.:0,0155759 3rd Qu.:130,0
Max. :0,0584113 Max. :141,0 # Modelo 1
model1 <- lm(dec ~ freq + angle + ch_length, data = air)
# Modelo 2 (mais complexo)
model2 <- lm(dec ~ freq + angle + ch_length + velocity + thickness, data = air)
# Comparando o RMSE dos dois modelos
RMSE <- function(error) { sqrt(mean(error^2)) } # Função para o Cálculo de RMSE
RMSE(model1$residuals) # RMSE modelo 1 = 5,216[1] 5,215778RMSE(model2$residuals) # RMSE modelo 2 = 4,799 (Melhor modelo)[1] 4,799244Clustering
Para o caso dos modelos que utilizam Clustering, usamos como base a distância métrica entre os pontos referentes a cada observação. O desempenho do modelo de clustering pode ser avaliado a partir de duas estatísticas principais:
- WSS (Within sum of squares): mede a similaridade dentro dos clusters. Quanto menor, mais similares são as observações dentro do cluster.
- BSS (Between cluster sum of squares): mede a similaridade entre os clusters. Quanto maior, menos similares são os clusters entre si.
Para resumir essas duas estatísticas, podemos dividir o WSS pelo BSS para verificar se a soma interna dos quadrados é substancialmente menor que a soma entre quadrados.
O código abaixo mostra um exemplo de como obter o WSS e o BSS para o banco de dados “Seeds”, que mostra várias características de 210 sementes distintas. Agruparemos os clusters via a função “kmeans()” (pacote “stats”).
summary(seeds) # Analisando o banco de dados area perimeter compactness length
Min. :10,59 Min. :12,41 Min. :0,8081 Min. :4,899
1st Qu.:12,27 1st Qu.:13,45 1st Qu.:0,8569 1st Qu.:5,262
Median :14,36 Median :14,32 Median :0,8734 Median :5,524
Mean :14,85 Mean :14,56 Mean :0,8710 Mean :5,629
3rd Qu.:17,30 3rd Qu.:15,71 3rd Qu.:0,8878 3rd Qu.:5,980
Max. :21,18 Max. :17,25 Max. :0,9183 Max. :6,675
width asymmetry groove_length
Min. :2,630 Min. :0,000077 Min. :4,519
1st Qu.:2,944 1st Qu.:2,561500 1st Qu.:5,045
Median :3,237 Median :3,599000 Median :5,223
Mean :3,259 Mean :3,688187 Mean :5,408
3rd Qu.:3,562 3rd Qu.:4,768750 3rd Qu.:5,877
Max. :4,033 Max. :8,456000 Max. :6,550 # Semente aleatória
set.seed(737)
# Usando a função kmeans() para agrupar o banco de dados em 3 clusters
if(!require(stats)){ install.packages("stats"); require(stats) }
km_seeds <- kmeans(seeds, 3)
# Plotando o gráfico e colorindo os ponto de acordo com os clusters formados
plot(length ~ compactness, data = seeds,col=km_seeds$cluster)
# Obtendo o WSS e o BSS
km_seeds$tot.withinss # WSS (Menor)[1] 600,2122km_seeds$betweenss # BSS (Maior)[1] 2136,149# Verificando a razão entre o WSS e o BSS
km_seeds$tot.withinss/km_seeds$betweenss[1] 0,2809786Training set e Test set no machine learning
Quando estamos utilizando técnicas de Machine Learning com aprendizado supervisionado, buscamos elaborar modelos com um forte poder preditivo. Isso nos permite fazer boas predições para novas observações.
Ao criarmos modelos preditivos, não devemos utilizar o banco de dados inteiro para “treinar” nosso modelo. Devemos separá-lo em duas partes diferentes (sem nenhuma observação em comum), conhecidas como:
- Training set: é a parte utilizada para “treinar” o modelo. Contém a maior parte das observações do banco de dados original. Embora não exista uma regra exata, o training set normalmente abrange cerca de 75% das observações do banco de dados original.
- Test set: é a parte do banco de dados utilizada para avaliar o desempenho do modelo, verificando se as predições realizadas pelo modelo treinado no training set foram similares ao valor real esperado. O test set abrange uma menor parte (por volta de 25%) do banco de dados original.
Abaixo, podemos ver um exemplo de como dividir um banco de dados em training e test set. Utilizaremos o banco de dados “titanic”, que possuía dados referentes as vítimas do desastre do Titanic. Embora o critério de separação das partes seja arbitrário, usaremos uma separação 75/25 para o traning/test set.
summary(titanic) # Analisando o banco de dados Survived Pclass Sex Age
Min. :0,0000 Min. :1,000 Length:714 Min. : 0,42
1st Qu.:0,0000 1st Qu.:1,000 Class :character 1st Qu.:20,12
Median :0,0000 Median :2,000 Mode :character Median :28,00
Mean :0,4062 Mean :2,237 Mean :29,70
3rd Qu.:1,0000 3rd Qu.:3,000 3rd Qu.:38,00
Max. :1,0000 Max. :3,000 Max. :80,00 # Semente aleatória
set.seed(252)
# "Embaralhando" os dados
n <- nrow(titanic) # número de linhas do banco original
Aleatorizado <- titanic[sample(n),]
# Separando os dados em training and test set
train_indices <- 1:round(0.75 * n) #separando a parte training que será retirada
train <- Aleatorizado[train_indices, ] # criando o train set (75% dos dados aleatorizado)
test_indices <- (round(0.75 * n) + 1):n #separando a parte test que será retirada
test <- Aleatorizado[test_indices, ] # criando o test set (25% dos dados aleatorizado)
train %>% dim() # 536 linhas[1] 536 4test %>% dim() # 178 linhas[1] 178 4Observações:
* Geralmente, quanto maior a quantidade de dados, melhor o modelo.
* É importante certificar que o test set não seja muito pequeno.
* Antes de se dividir o banco de dados, é interessante também embaralhar o conjunto dados. Essa mistura pode afetar o desempenho do modelo, então é sugerida a utilização de uma técnica conhecida como cross-validation.
* A ideia do cross-validation é utilizar um algoritmo que testa o modelo diversas vezes, utilizando diferentes partes dos dados. Dessa maneira, usam-se os diversos resultados obtidos em cada um dos testes para obter uma medida final mais robusta.

Bias e Variância
O Bias e a Variância são elementos chave para a avaliação de modelos no Machine Learning. Ao utilizarmos o aprendizado supervisionado, temos como objetivo principal a predição dos dados, o que pode ocasionar erros de predição. Esses erros são divididos em erros irreduzíveis (“noise”) e reduzíveis. Estes são divisíveis em erros gerados pelo Bias e erros gerados pela Variância.
- Erro pelo Bias: ocasionado pelo uso de suposições incorretas, como a distribuição estatística seguida pelos dados. Um aumento no número de restrições impostas no modelo dentro do training set ocasiona um aumento do erro gerado pelo Bias. Isso acontece porque o modelo procura uma forma de generalizar as suposições, gerando um fenômeno conhecido como Underfit.
- Erro pela Variância: ocasionado quando o modelo se adequa de forma muito exagerada ao training set. Ao se adaptar de uma forma muito melhor no training set do que no test set, o modelo se torna muito específico para dados que possuem um comportamento similar ao traning set. Assim não consegue predizer bem dados menos específicos, gerando um fenômeno conhecido como Overfit.

Um aumento no erro devido ao Bias ocasiona uma diminuição no erro devido a Variância nesse mesmo modelo e vice-versa.
Classificação no Machine Learning
A Classificação é uma subárea do Machine Learning que atribui uma classe para uma nova observação a partir de diversas características/variáveis de observações passadas. Essa classificação pode ser binária (duas classes, 1 ou 0) ou multiclasse (três ou mais classes).
Exemplo: Classificar pessoas como “Feliz” ou “Não feliz” com base nas características “idade”, “salário” e “altura”. Todas as observações do banco de dados devem apresentar tais características, assim como as novas observações onde iremos realizar a previsão.
Árvore de Decisões
A árvore de decisões é uma técnica utilizada para Classificação e consiste em um mapa dos possíveis resultados de uma série de escolhas. Essas escolhas estão relacionadas a diversas decisões tomadas com base nas variáveis do banco de dados utilizado. A árvore de decisões é formada por 3 partes principais:
- Raiz: é a primeira decisão a ser tomada pelo usuário. A partir dela as pessoas são redirecionadas a outras decisões, de acordo com sua escolha nessa questão.
- Nós: são todas as decisões apresentadas na árvore.
- Folhas: são os resultados da árvore de decisões. É nela que a classificação é realizada.

É importante entender que utilizamos o Traning Set para a construção da Árvore de Decisões. Após cada decisão, o Training Set é dividido em partes menores que seguem o critério da decisão. Dessa forma, o Training Set será dividido até que cada uma das “folhas” contenha apenas uma pequena parte do Traning Set original . O critério utilizado para a divisão do Training Set é o ganho de informação. Então separam-se os dados com base no teste (Yes/No) que será aplicado na próxima decisão, escolhendo o teste que apresente a divisão mais heterogênea entre as classes. Garantindo assim o maior ganho de informação.
No código abaixo, iremos construir uma árvore de decisões binária (Yes = 1 e No = 0) usando como base o banco de dados titanic, que possuía dados referentes às vítimas do desastre do Titanic. Usaremos a função rpart() (pacote “rpart”) para a criação da árvore de decisões e uma função chamada “fancyRpartPlot()” (pacote “rattle”) para a plotagem da árvore. O Training Set e o Test Set já foram separados anteriormente.
# Semente Aleatória
set.seed(320)
# Carregando os pacotes necessários
if(!require(rpart)){ install.packages("rpart"); require(rpart) } # Construção da árvore
if(!require(rattle)){ install.packages("rattle"); require(rattle) } # Plotagem estilizada da arvore
if(!require(rpart.plot)){ install.packages("rpart.plot"); require(rpart.plot) } # Auxiliador na plotagem do gráfico
if(!require(RColorBrewer)){ install.packages("RColorBrewer"); require(RColorBrewer) } # Cores árvore
# Contruindo a arvoré a partir do train set com todas as variáveis.
summary(train) Survived Pclass Sex Age
0:295 1:132 female:180 Min. : 0,83
1:205 2:133 male :320 1st Qu.:21,00
3:235 Median :28,00
Mean :30,11
3rd Qu.:38,25
Max. :80,00 tree <- rpart(Survived ~ ., train, method="class") # Método = Classificação
# Plotando a arvore de decisoes
fancyRpartPlot(tree) # Esquerda = Sim, Direita = Não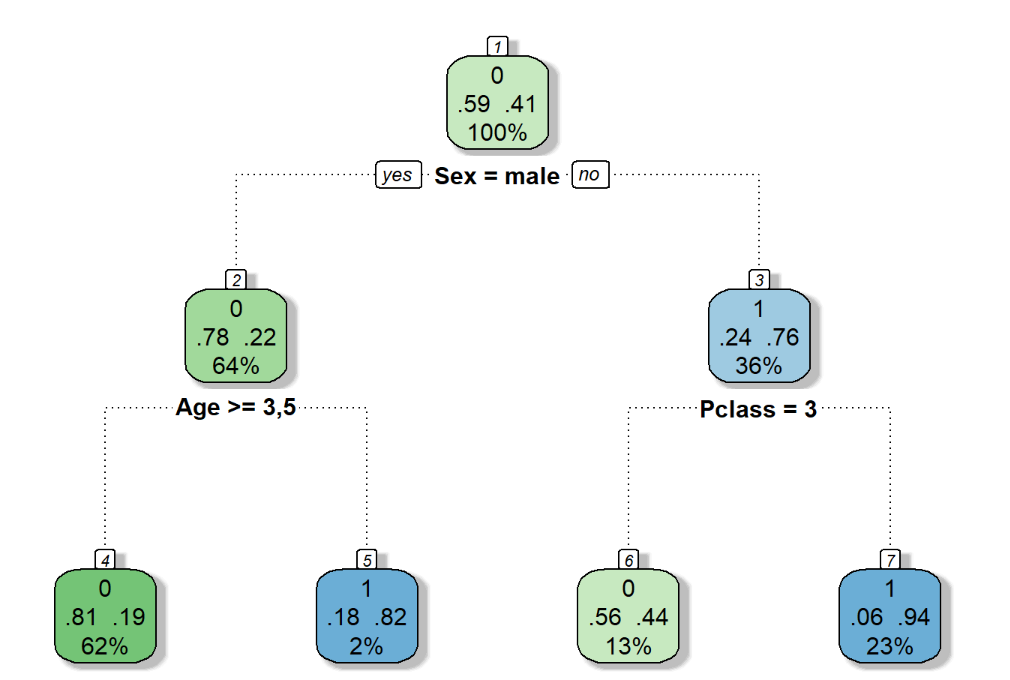
Para que possamos entender melhor o que cada nó representa, vamos analisar a imagem abaixo. Ela apresenta o nó referente aos indivíduos que responderam “Não” à decisão “Male?” (ou seja, tratava-se de uma pessoa do sexo feminino). Quando separamos o Training Set entre os nós, nem todas as categorizações seguem a classificação que desejamos (se o passageiro sobreviveu ou não). O número “.76” mostra que 76% dos indivíduos do sexo feminino foram responsáveis pela classificação 1 (“Sobreviveu”). Sendo essa a classificação de maior frequência apresentada acima das porcentagens (o número “1”). O número “36%” mostra que 36% de todo conjunto de treinamento passa por esse nó específico. Por fim, o texto “Pclass = 3” indica o próximo teste que será aplicado para a nova separação desse nó.
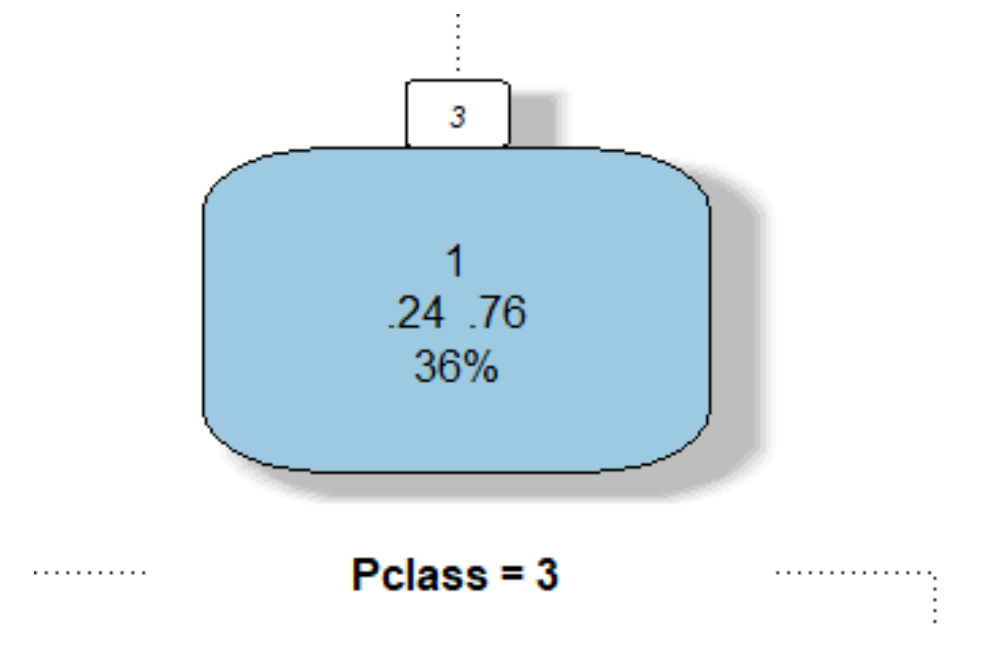
É possível também tentar “podar” a árvore de decisões, aumentando ou diminuindo sua complexidade. Um aumento excessivo na complexidade gera uma árvore muito grande e um Overfit, já que ela é muito específica. Podemos usar a função prune() (pacote “rpart”) para podar a árvore, diminuindo seu tamanho e aumentando seu Bias. O exemplo abaixo apresenta essa ideia.
### Podemos aumentar a complexidade da arvoré de decisões usando o parâmetro control
tree.complex <- rpart(Survived ~ ., train, method = "class", control = rpart.control(cp=0.00001))
# Plotando - a árvore aumento muito sua Variância - Fenômeno de Overfit
fancyRpartPlot(tree.complex)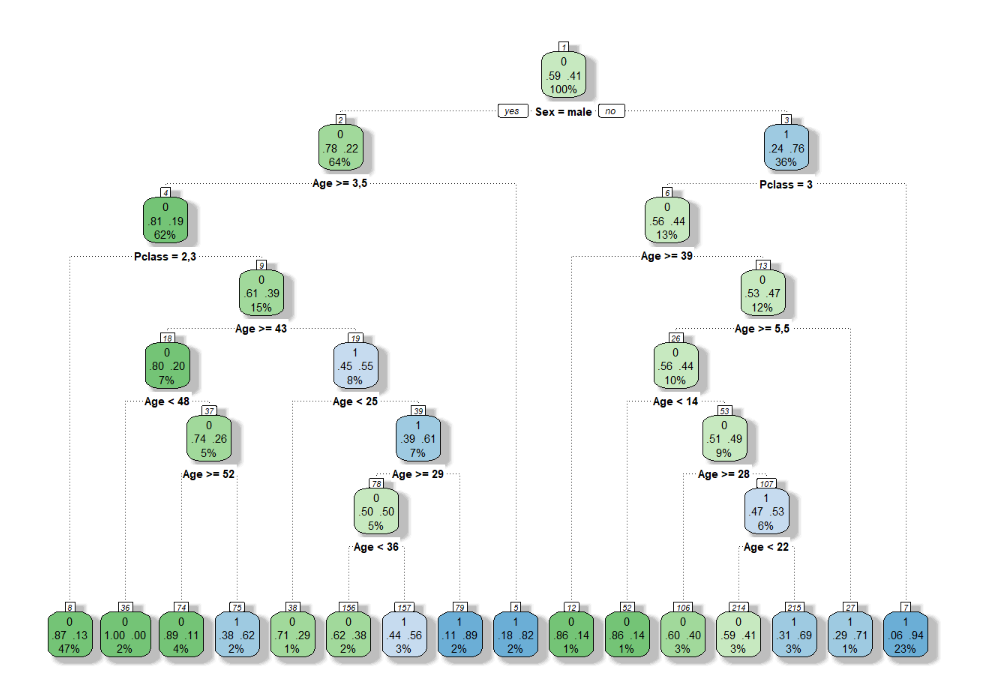
# Podando a arvore - função prune()
Pruned <- prune(tree.complex,cp=0.01) # Reduzimos muito a complexidade (cp = 0.01)
# Plotando a árvore podada (menos complexa)
fancyRpartPlot(Pruned) 
k-Nearest Neighbors
Outro método da classificação na área do Machine Learning é o método do “K-nearest Neighbors”. Nesse método, utiliza-se a distância (usualmente a Euclidiana) entre uma nova observação e as demais observações de um training set para classificá-la de acordo com a observação mais próxima. O “k” determina o número de vizinhos que serão utilizados para a classificação. Por exemplo, se k=5, utilizaremos os 5 vizinhos mais próximos da nova observação e a classificaremos com base na classe mais frequente dentre esses vizinhos.
É importante verificar se os parâmetros utilizados seguem uma mesma medida e, em caso negativo, escaloná-los para que o cálculo da distância não seja afetado.
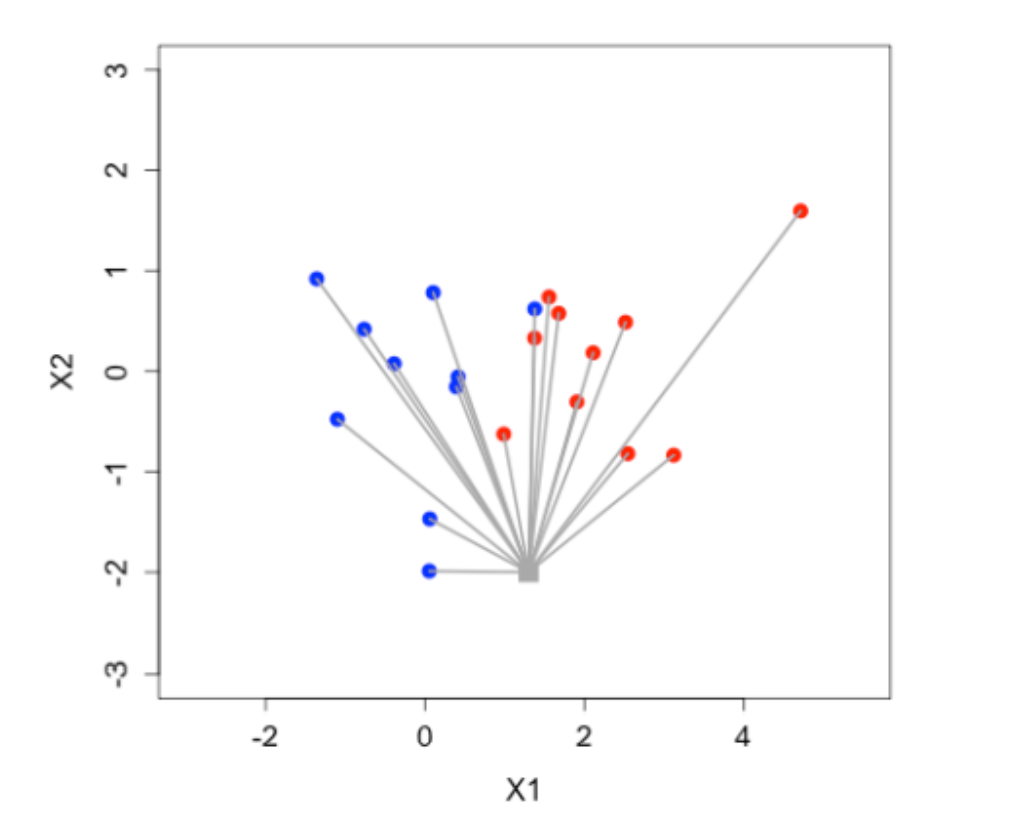
O código abaixo trabalha com o banco de dados titanic, com os seus Training sets já carregados. Usaremos a função knn() (pacote “class”) para realizar o método do K-nearest Neighbors, com k = 5 vizinhos. Calcularemos também a matriz de confusão para esse problema para avaliarmos nosso modelo.
# Semente Aleatória
set.seed(231)
# Retirando as classificações de interesse do training and test set
train_labels<- train$Survived
test_labels<- test$Survived
# Construindo as variáveis que serão utilizadas no Knn
knn_train <- train
knn_test <- test
# zerando as colunas das variáveis
knn_train$Survived <- NULL
knn_test$Survived <- NULL
# Escalonando a Classe dos passageiros via Normalização
min_class <- min(knn_train$Pclass)
max_class <- max(knn_train$Pclass)
knn_train$Pclass <- (knn_train$Pclass - min_class) / (max_class - min_class)
knn_test$Pclass <- (knn_test$Pclass - min_class) / (max_class - min_class)
# Escalonando a idade dos passageiros via Normalização
min_age <- min(knn_train$Age)
max_age <- max(knn_train$Age)
knn_train$Age <- (knn_train$Age - min_age) / (max_age - min_age)
knn_test$Age <- (knn_test$Age - min_age) / (max_age - min_age)
# Transformando o sexo dos individuos em 0 ou 1 para o calculo da distancia
knn_train$Sex <- case_when(knn_train$Sex == "male" ~ 1,
TRUE ~ 0)
knn_test$Sex <- case_when(knn_test$Sex == "male" ~ 1,
TRUE ~ 0)
# Carregando o pacore e aplicando o KNN para k=5
if(!require(class)){ install.packages("class"); require(class) }
prev <- class::knn(train = knn_train, test = knn_test, cl = train_labels, k = 5)
# Matriz de Confusão - Valores reais nas linhas e previsões nas colunas
conf<- table(test_labels,prev)
conf prev
test_labels 0 1
0 113 16
1 26 59# Calculando o TP, FN, FP e TN
TN <- conf[1, 1] # 113
FN <- conf[2, 1] # 26
FP <- conf[1,2] # 16
TP <- conf[2,2] # 59
# Cálculo da Acurácia = 80,37 %
acc <- (TP + TN)/(TP+TN+FP+FN)
acc[1] 0,8037383# Calculo da precisão = 78,67 %
prec <- TP/(TP+FP)
prec[1] 0,7866667# Calculo Recall = 69,41 %
rec <- TP/(TP+FN)
rec[1] 0,6941176Curva ROC
A curva ROC é uma curva construída com base em uma classificação binária. É uma medida de desempenho muito poderosa e usa como base as probabilidades retiradas de uma matriz de confusão:

Dado essas estatísticas, construímos uma curva utilizando o FPR do modelo no eixo x e o TPR no eixo y. E seus valores são calculados utilizando diversos limiares de classificação (porcentagem que denomina se um indivíduo é positivo ou negativo). Por exemplo, o início da curva representa um limiar onde todos os indivíduos são negativos, visto que seu FPR e seu TPR são iguais a 0%. Já o final da curva representa um limiar onde todos os indivíduos são classificados como positivos, visto que tanto o seu FPR quando seu TPR são iguais a 1 (100%).
Uma maneira de interpretar a curva ROC é a seguinte: quando mais próxima a curva estiver do canto superior esquerdo do gráfico, melhor o desempenho do modelo testado. Visto que obteremos um True Positive Rate mais próximo de 100% e um False Positive Rate mais próximo de 0%. Em outras palavras, classificadores bons apresentam uma área maior abaixo da curva, chamada também como AUC. Usualmente, uma AUC superior a 0,9 é considerada muito boa. Caso o objetivo seja comparar dois métodos (ou mais) distintos, basta compararmos as AUC’s dos métodos: o método que apresentar maior AUC será o de melhor desempenho dentre os demais.
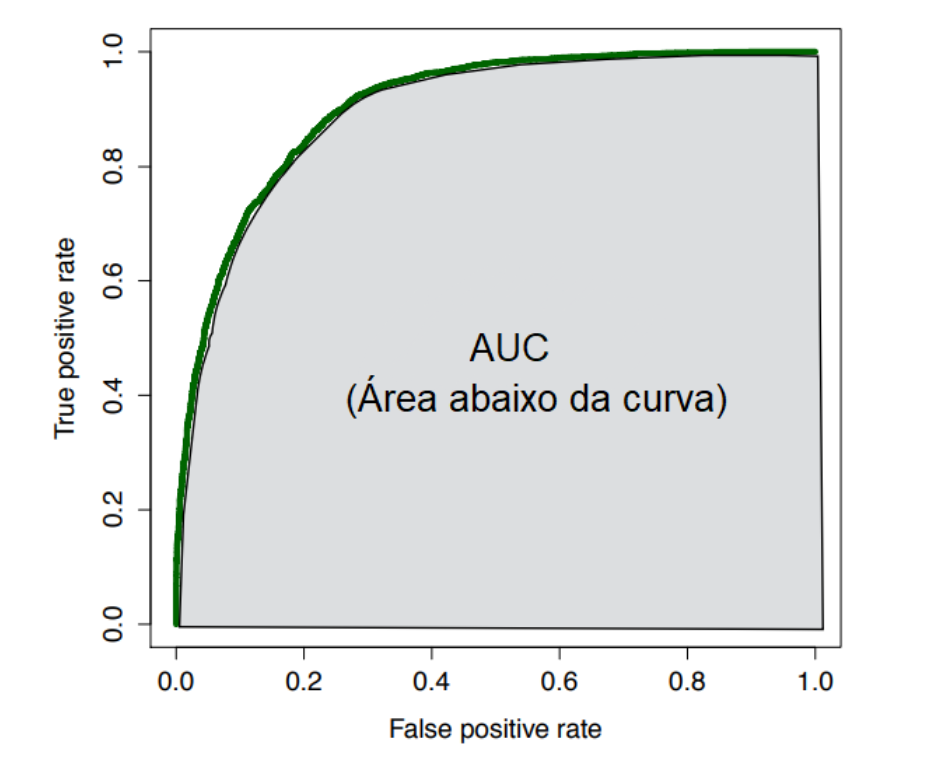
O código abaixo utiliza como uma base de dados chamada “income”, responsável por classificar o salário anual de seus indivíduos de forma binária: em 0 (menor que 50 mil dólares) ou 1 (igual ou maior a 50 mil dólares) com base em diversas características deles, como raça, escolaridade e sexo. Carregaremos o training and test set desse banco de dados já construídos e focaremos na utilização da função performance() (pacote “ROCR”) para calcular as estatísticas TPR, FPR e AUC de um modelo baseado em uma árvore de decisões para a construção da curva ROC.
# Semente Aleatória
set.seed(449)
# Construindo uma árvore de decisões para a classificação e retirando a prob. da predição ser igual a 1 para cada observação
tree <- rpart(income ~ ., income.train, method = "class") # Método = classificação
probs <- predict(tree, income.test, type = "prob")[,2] # predict(Modelo, local onde deve ocorrer a predição, tipo de predição)
# Carregando o pacote ROCR para a criação da curva ROC
if(!require(ROCR)){ install.packages("ROCR"); require(ROCR) }
# Criando um objeto de previsão para a curva ROC, transformando as probabilidades em um formato padronizado
pred <- prediction(probs,income.test$income)
# Criando um objeto de desempenho para a curva ROC - True e False positive Rate
perf.rates <- performance(pred,"tpr","fpr")
# Plotando a curva ROC
plot(perf.rates)
# Podemos também calcular o AUC utilizando como parâmetro "auc"
perf.auc <- performance(pred,"auc")
# AUC do modelo
perf.auc@y.values[[1]] [1] 0,8463732No artigo da semana que vem continuaremos falando sobre machine learning, só que agora focando em Regressão e Clustering. Siga a Oper nas redes sociais e não perca nenhum artigo! Estamos no Instagram, LinkedIn e Facebook.