Artigo escrito com a colaboração de Carolina Jacomini Sampaio
A análise de dados envolvendo variáveis qualitativas, que lidam com categorias ou grupos distintos, exige cuidados especiais na escolha dos métodos estatísticos. Quando se busca comparar diferentes grupos ou amostras, é fundamental adotar técnicas adequadas para garantir resultados robustos e significativos. Este artigo tem como objetivo explorar os principais métodos de comparação para variáveis qualitativas, discutindo suas vantagens, limitações e as melhores aplicações práticas.
Entre os métodos mais utilizados para comparar variáveis qualitativas estão os testes de qui-quadrado e as análises baseadas na probabilidade, que permitem avaliar a associação entre categorias. A escolha entre essas técnicas depende de fatores como o tamanho das amostras, a distribuição dos dados e o objetivo da análise. A compreensão desses métodos é crucial para garantir a confiabilidade dos resultados e suas implicações nas tomadas de decisão. De acordo com o quadro abaixo, nota-se os pressupostos de utilização de cada teste.

O primeiro passo para saber qual teste usar em uma comparação de médias entre variáveis qualitativas é verificar se o objetivo do problema é avaliar o grau de concordância entre dois ou mais indivíduos, ou avaliar a associação entre as repostas dos indivíduos.
Teste de concordância
Teste Kappa
O coeficiente de concordância de Kappa é utilizado para descrever a concordância entre dois ou mais juízes quando realizam uma avaliação nominal ou ordinal de uma mesma amostra. Por meio dos dados tem-se a seguinte tabela:
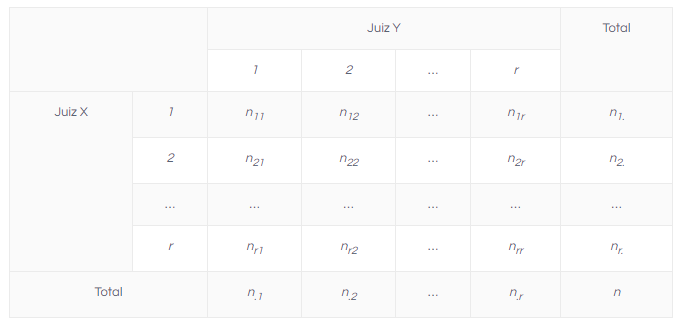
Nos quais:
- r representa as categorias de avaliação;
- n(ij) representa a quantidade de elementos amostrais avaliados pelo juiz X na categoria i e pelo juiz Y na categoria j ;
- n.i representa a quantidade de elementos amostrais avaliados pelo juiz Y na categoria i ;
- ni. representa a quantidade de elementos amostrais avaliados pelo juiz X na categoria j ;
- n representa o total de elementos amostrais avaliados.
O valor do coeficiente de concordância de Kappa pode variar de:
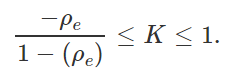
Isso considerando que:
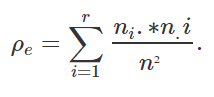
As hipóteses do teste são:
Ho: A concordância entre os juízes foi puramente aleatória.
Ha: A concordância entre os juízes não foi puramente aleatória.
Exemplo:
Dois médicos não identificados avaliam de forma independente o resultado de exames de diagnóstico por imagem de 180 pacientes e os classificam como “normal”, “alterado” e “inconclusivo”.
Pacientes <- c(1:180)
Medico.X <- c("Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal","Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado","Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Inconclusivo", "Normal", "Normal", "Inconclusivo")
Medico.X <- factor(Medico.X,
levels = c("Normal", "Alterado", "Inconclusivo"))
Medico.Y <- c("Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Normal", "Normal", "Alterado", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Normal", "Normal", "Alterado", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Normal", "Alterado", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Alterado", "Inconclusivo", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Normal", "Alterado", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Normal", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Alterado", "Alterado", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Normal", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Alterado", "Alterado", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Normal", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Alterado", "Inconclusivo", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Normal", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Alterado", "Inconclusivo", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Normal", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Alterado", "Inconclusivo", "Alterado",
"Normal", "Alterado", "Inconclusivo", "Normal", "Alterado", "Inconclusivo",
"Normal", "Normal", "Normal", "Normal", "Inconclusivo", "Normal",
"Normal", "Inconclusivo", "Alterado", "Alterado", "Inconclusivo", "Alterado")
Medico.Y <- factor(Medico.Y,
levels = c("Normal", "Alterado", "Inconclusivo"))
Dados <- data.frame(Pacientes, Medico.X, Medico.Y)
head(Dados)## Pacientes Medico.X Medico.Y
## 1 1 Normal Normal
## 2 2 Alterado Alterado
## 3 3 Inconclusivo Inconclusivo
## 4 4 Normal Normal
## 5 5 Alterado Alterado
## 6 6 Inconclusivo InconclusivoAo organizar os dados como na tabela teórica, tem-se a seguinte tabela:
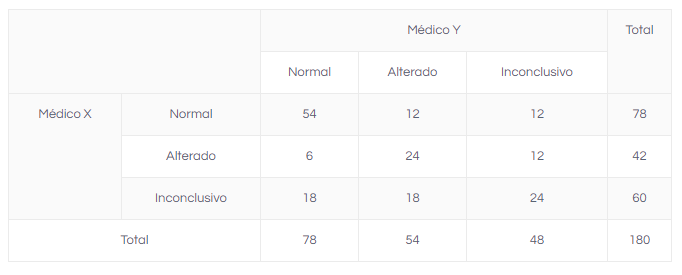
Portanto:
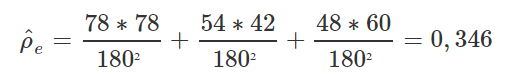
E os valores de K podem variar de -0,529 até 1, para esses dados. Portanto, classificamos o valor de K de acordo com a seguinte tabela:
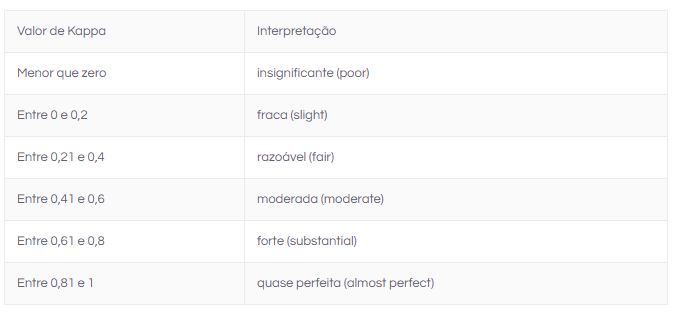
Para realizar o teste Kappa no R, entrando com as variávies, é necessário instalar o pacote irr.
if(!require(irr)){install.packages("irr"); require(irr)}
head(Dados[,-1])## Medico.X Medico.Y
## 1 Normal Normal
## 2 Alterado Alterado
## 3 Inconclusivo Inconclusivo
## 4 Normal Normal
## 5 Alterado Alterado
## 6 Inconclusivo Inconclusivokappa2(Dados[,-1])## Cohen's Kappa for 2 Raters (Weights: unweighted)
##
## Subjects = 180
## Raters = 2
## Kappa = 0.337
##
## z = 6.39
## p-value = 1.67e-10Portanto, considerando α=0,05, a hipótese de que a concordância entre os médicos X e Y fosse puramente aleatória foi rejeitada já que o valor-p foi menor que 0,001. Além disso, ao utilizar a tabela de interpretação para o valor de kappa é possível concluir que como K^=0,337, a concordância entre os médicos X e Y em relação aos diagnósticos a partir dos exames de imagem foi razoável.
Uma outra maneira de realizar o teste é entrando com a tabela e não com as variávies. Nesse caso utiliza-se o pacote fmsb
if(!require(fmsb)){install.packages("fmsb"); require(fmsb)}
Tabela.kappa <- table(Dados$Medico.X, Dados$Medico.Y)
Tabela.kappa.2 <- as.matrix(Tabela.kappa,
dimnames = list("Medico X", "Medico Y"))
Tabela.kappa##
## Normal Alterado Inconclusivo
## Normal 54 12 12
## Alterado 6 24 12
## Inconclusivo 18 18 24Kappa.test(Tabela.kappa)## $Result
##
## Estimate Cohen's kappa statistics and test the null hypothesis that
## the extent of agreement is same as random (kappa=0)
##
## data: Tabela.kappa
## Z = 6.2021, p-value = 2.787e-10
## 95 percent confidence interval:
## 0.2259316 0.4475378
## sample estimates:
## [1] 0.3367347
##
##
## $Judgement
## [1] "Fair agreement"O resultado é o mesmo nas duas funções.
Teste de associação
Caso o teste seja de associação, o próximo passo é verificar se as amostras são pareadas. Uma amostra é pareada quando um único juiz avalia o mesmo objeto de estudo em circunstâncias diferentes.
Amostras pareadas
Teste de McNemar
O Teste de McNemar é aplicado para tabelas de contingência 2×2 com um traço dicotômico, com pares de indivíduos correspondentes, para determinar as linhas e colunas onde as frequências marginais são iguais (isto é, se há uma “homogeneidade marginal”). Portanto, tem-se uma tabela como a seguinte figura:
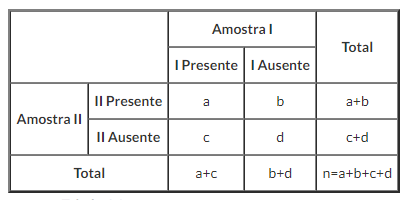
Além disso, as hipóteses do teste são:
Ho: As proporções marginais são iguais umas das outras.
Ha: As proporções marginais são diferentes umas das outras.
Exemplo:
Foi realizada uma pesquisa de opinião sobre o mandato do atual presidente dos Estados Unidos nesse mês e no mês passado, com uma amostra aleatória de 1600 eleitores americanos, para avaliar se os eleitores aprovam ou disaprovam o governo atual. Para realizar as análises no R é necessário apenas o pacote stats
if(!require(stats)){install.packages("stats"); require(stats)}
Performance <- matrix(c(794, 86, 150, 570),
nrow = 2,
dimnames = list("1ª Pesquisa" = c("Aprova", "Disaprova"),
"2ª Pesquisa" = c("Aprova", "Disaprova")))
Performance## 2ª Pesquisa
## 1ª Pesquisa Aprova Disaprova
## Aprova 794 150
## Disaprova 86 570mcnemar.test(Performance)##
## McNemar's Chi-squared test with continuity correction
##
## data: Performance
## McNemar's chi-squared = 16.818, df = 1, p-value = 4.115e-05Considerando α=0,05, a hipótese nula foi rejeitada já que o valor-p foi menor que 0,001. Portanto, os eleitores mudaram de opinião sobre o governo da 1ª para a 2ª pesquisa. Sendo que, a maior parte dos eleitores que mudaram de opinião anteriormente aprovavam o governo e passaram a desaprovar.
Amostras não pareadas
Caso as amostras não sejam pareadas, a última pergunta a se fazer é se o tamanho amostral é suficiente ou não.
Tamanho amostral suficiente
Teste Qui-quadrado
O Teste Qui-quadrado é um teste de homogeneidade que compara a distribuição de contagens para dois ou mais grupos usando a mesma variável categórica. Também pode ser usado para testar a qualidade de ajuste do modelo (aderência) e para testar independência.
Exemplo:
Uma rede de lojas que comercializa produtos de maquiagem tem franquias em três bairros de Belo Horizonte, uma em cada bairro. Sua gerente decidiu verificar se a satisfação dos clientes que realizaram compras no mês de março oscilavam em virtude da loja.
Bairro <- c("Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia",
"Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia",
"Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia",
"Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia",
"Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia", "Santa Efigênia",
"Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza",
"Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza",
"Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza",
"Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza", "Santa Tereza",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta",
"Floresta", "Floresta", "Floresta", "Floresta", "Floresta")
Bairro <- factor(Bairro,
levels = c("Floresta", "Santa Efigênia", "Santa Tereza"))
Satisfação <- c("Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito", "Satisfeito",
"Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito",
"Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito",
"Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito",
"Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito",
"Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito",
"Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito", "Insatisfeito")
Satisfação <- factor(Satisfação,
levels = c("Satisfeito", "Insatisfeito"))
Dados.chisq <- data.frame(Satisfação, Bairro)
table(Dados.chisq$Satisfação, Dados.chisq$Bairro)##
## Floresta Santa Efigênia Santa Tereza
## Satisfeito 30 20 15
## Insatisfeito 25 5 5tabela.aderencia(Dados.chisq$Bairro, Dados.chisq$Satisfação, 2, "chisq")## N % N % Valor_p
## Floresta 30 0.4615385 25 0.7142857 0.0499365
## Santa Efigênia 20 0.3076923 5 0.1428571 0.0499365
## Santa Tereza 15 0.2307692 5 0.1428571 0.0499365Considerando α=0,05, a hipótese nula é rejeitada já que o valor-p foi igual a 0,0499. Portanto, a satisfação dos clientes que realizaram compras no mês de março oscilavam em virtude da loja. Sendo que a franquia do bairro Floresta apresentou o maior percentual de insatisfação com as compras do mês de março se comparado com as demais lojas.
Tamanho amostral insuficiente
Teste Exato de Fisher
O teste exato de Fisher é um teste de significância estatística, utilizado na análise de tabelas de contingência. Embora, na prática, ele seja empregado quando os tamanhos das amostras são pequenos, é válido para todos os tamanhos de amostra.
Esse teste pertence a uma classe de testes exatos. Eles são chamados assim por conta da significância do desvio de uma hipótese nula (e.g., p-valor) que pode ser calculada exatamente, ao invés de depender de uma aproximação que se torna exata no limite conforme o tamanho da amostra cresce para o infinito, como em muitos testes estatísticos.
Fisher disse ter concebido o teste depois de um comentário da Dra. Muriel Bristol, que afirmou ser capaz de detectar se o chá ou o leite foi adicionado primeiro em sua xícara. Ele testou seu pedido no experimento “dama apreciadora de chá”.
Ele é um teste de homogeneidade, mas também pode testar aderência ou independência.
Exemplo:
De maneira geral, os doentes psiquiátricos podem ser classificados em psicóticos e neuróticos. Um psiquiatra realiza um estudo sobre os sintomas suicidas em duas amostras de 20 doentes de cada grupo. A nossa hipótese é que a proporção de psicóticos com sintomas suicidas é igual a proporção de neuróticos com esses sintomas.
Doente <- c("Psicótico", "Psicótico", "Psicótico", "Psicótico", "Psicótico",
"Psicótico", "Psicótico", "Psicótico", "Psicótico", "Psicótico",
"Neurótico", "Neurótico", "Neurótico", "Neurótico", "Neurótico",
"Neurótico", "Neurótico", "Neurótico", "Neurótico", "Neurótico")
Doente <- factor(Doente,
levels = c("Psicótico", "Neurótico"))
Sintomas.suicidas <- c("Presente", "Ausente", "Ausente", "Ausente", "Ausente",
"Ausente", "Ausente", "Ausente", "Ausente", "Ausente",
"Presente", "Presente", "Ausente", "Ausente", "Ausente",
"Presente", "Presente", "Ausente", "Ausente", "Ausente")
Sintomas.suicidas <- factor(Sintomas.suicidas,
levels = c("Presente", "Ausente"))
Dados.fisher <- data.frame(Sintomas.suicidas, Doente)
table(Dados.fisher$Sintomas.suicidas, Dados.fisher$Doente)##
## Psicótico Neurótico
## Presente 1 4
## Ausente 9 6tabela.aderencia(Dados.fisher$Sintomas.suicidas, Dados.fisher$Doente, 2, "chisq")## Warning in chisq.test(t0): Chi-squared approximation may be incorrect## N % N % Valor_p
## Presente 1 0.1 4 0.4 0.3016996
## Ausente 9 0.9 6 0.6 0.3016996tabela.aderencia(Dados.fisher$Sintomas.suicidas, Dados.fisher$Doente, 2, "fisher")## N % N % Valor_p
## Presente 1 0.1 4 0.4 0.3034056
## Ausente 9 0.9 6 0.6 0.3034056Considerando α=0,05, a hipótese nula não rejeitada já que o valor-p foi igual a 0,235. Portanto, a proporção de psicóticos com sintomas suicidas é igual à proporção de neuróticos com esses sintomas.
Teste Qui-quadrado Simulado
Caso os testes Qui-quadrado e/ou exato de Fisher apresentem uma mensagem de que a aproximação do teste deve estar incorreta, usa-se o Teste Qui-quadrado Simulado. Essa mensagem geralmente aparece quando algumas das caselas da tabela apresenta valor muito baixo em comparação com os demais.
tabela.aderencia(Dados.fisher$Sintomas.suicidas, Dados.fisher$Doente, 2, "chisq.simulate")## N % N % Valor_p
## Presente 1 0.1 4 0.4 0.2994701
## Ausente 9 0.9 6 0.6 0.2994701Ainda ficou alguma dúvida? Deixe seu comentário que vamos responder.
Curtiu nosso conteúdo? Você encontra muito mais no canal do Statplace no YouTube. Siga-nos nas redes sociais! Estamos no Facebook, Instagram e LinkedIn.




1 comentário em “Comparação de médias entre variáveis qualitativas”
Thank you for your sharing. I am worried that I lack creative ideas. It is your article that makes me full of hope. Thank you. But, I have a question, can you help me?